Mixed Models: part two

Announcements

Mixed Effects Models this week (lab) –> One “lab” with me

Next week: Generalized Mixed Effects Models (No Lab)

Next week (Friday): Work on your plot

Back to our example

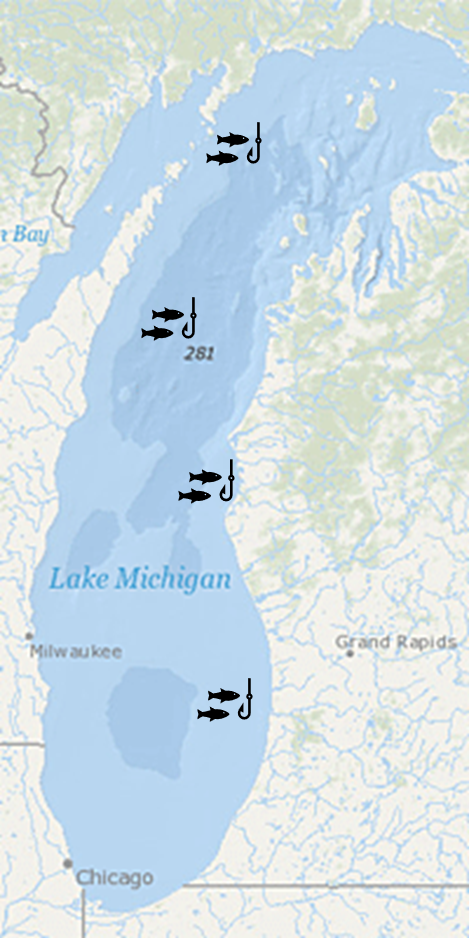
Back to our example

  • We set 4 nets

  • Sites were randomly chosen

  • We are interested in the content of Hg in Walleye

  • Hg is correlated with size. The bigger the fish, the higher Hg content it has

  • So, normally we could do one thing:

  • \(E[Hg_i] = \beta_0 + \beta_1 \times size_{i}\)

  • \(y_i \sim N(mean = E[Hg_i], \sigma)\)

Linear model

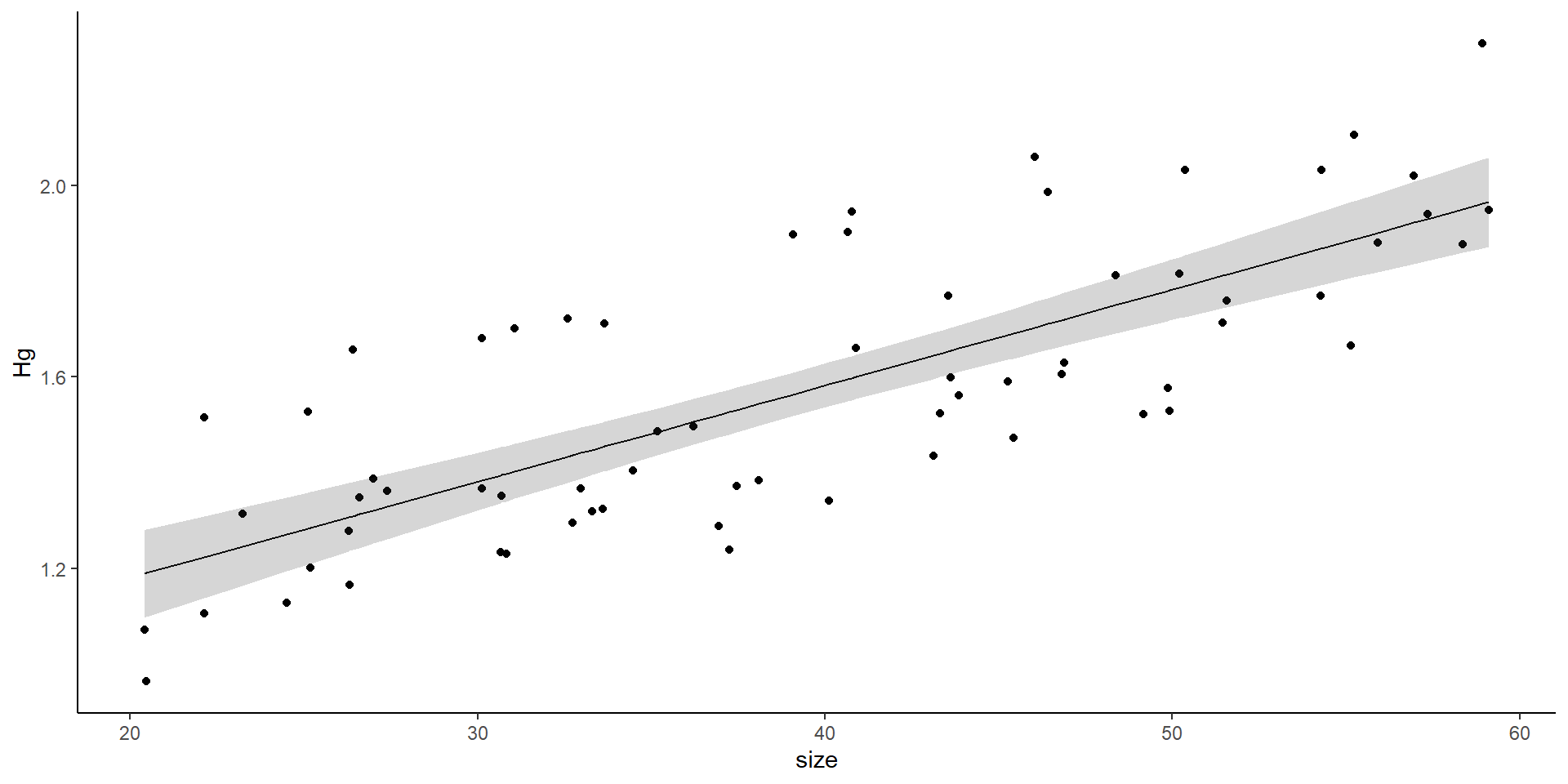
Linear model


Call:
lm(formula = Hg ~ size, data = HgDat_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.28712 -0.13507 -0.05476  0.10644  0.35471 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.781644   0.084717   9.227 1.98e-13 ***
size        0.020017   0.002067   9.682 3.16e-14 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1874 on 65 degrees of freedom
Multiple R-squared:  0.5905,    Adjusted R-squared:  0.5843 
F-statistic: 93.75 on 1 and 65 DF,  p-value: 3.165e-14

  • Use coefficients to estimate size at over 1.1 \(\mu g\) .

  • Limit fish of that size

Assumptions of a Linear Model

Normality

Homoschedasticity

Linearity

Independence –> of data

Independence –> of error (or residuals)

Linear Model

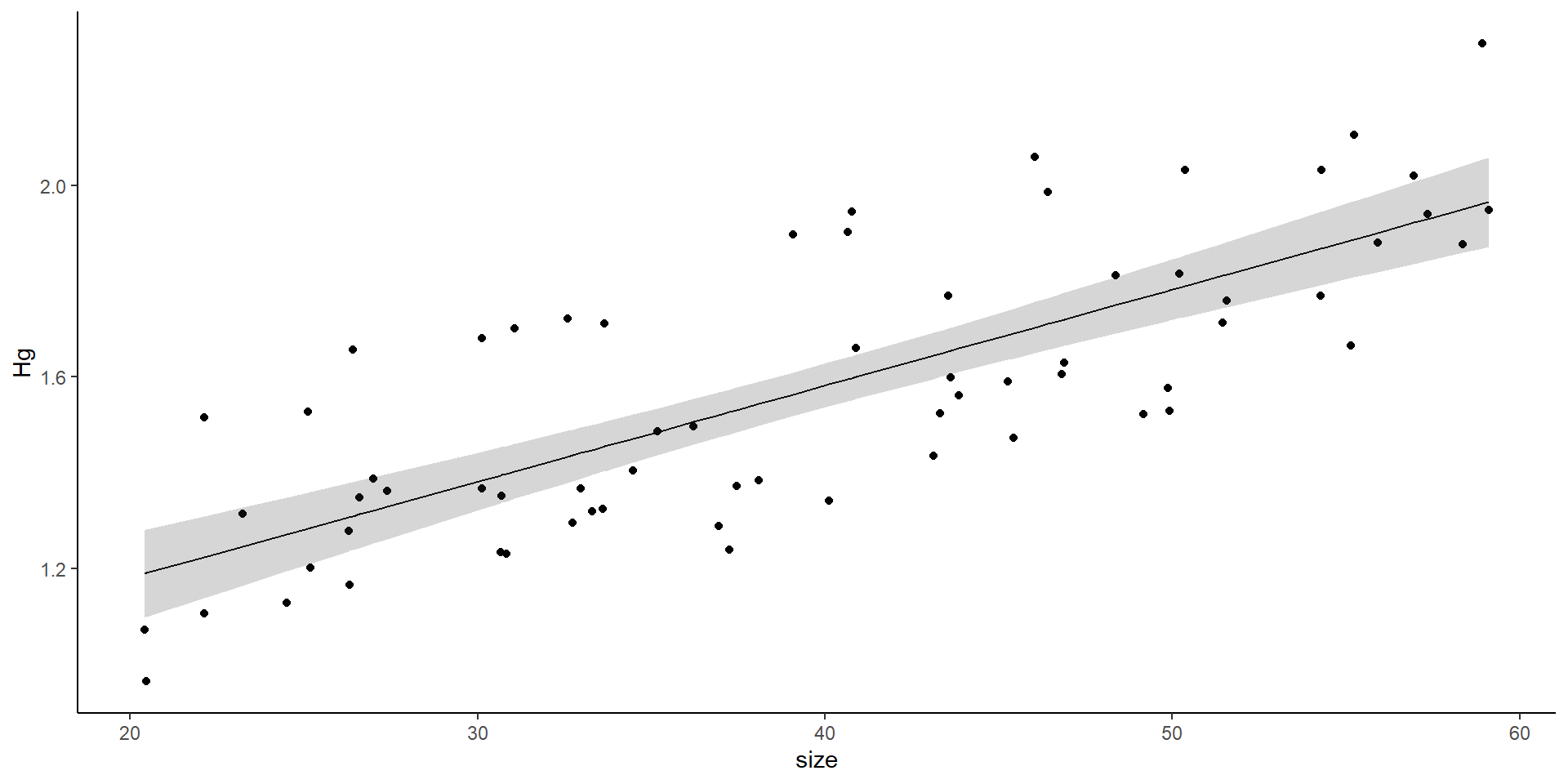
If we plot the “sites”?

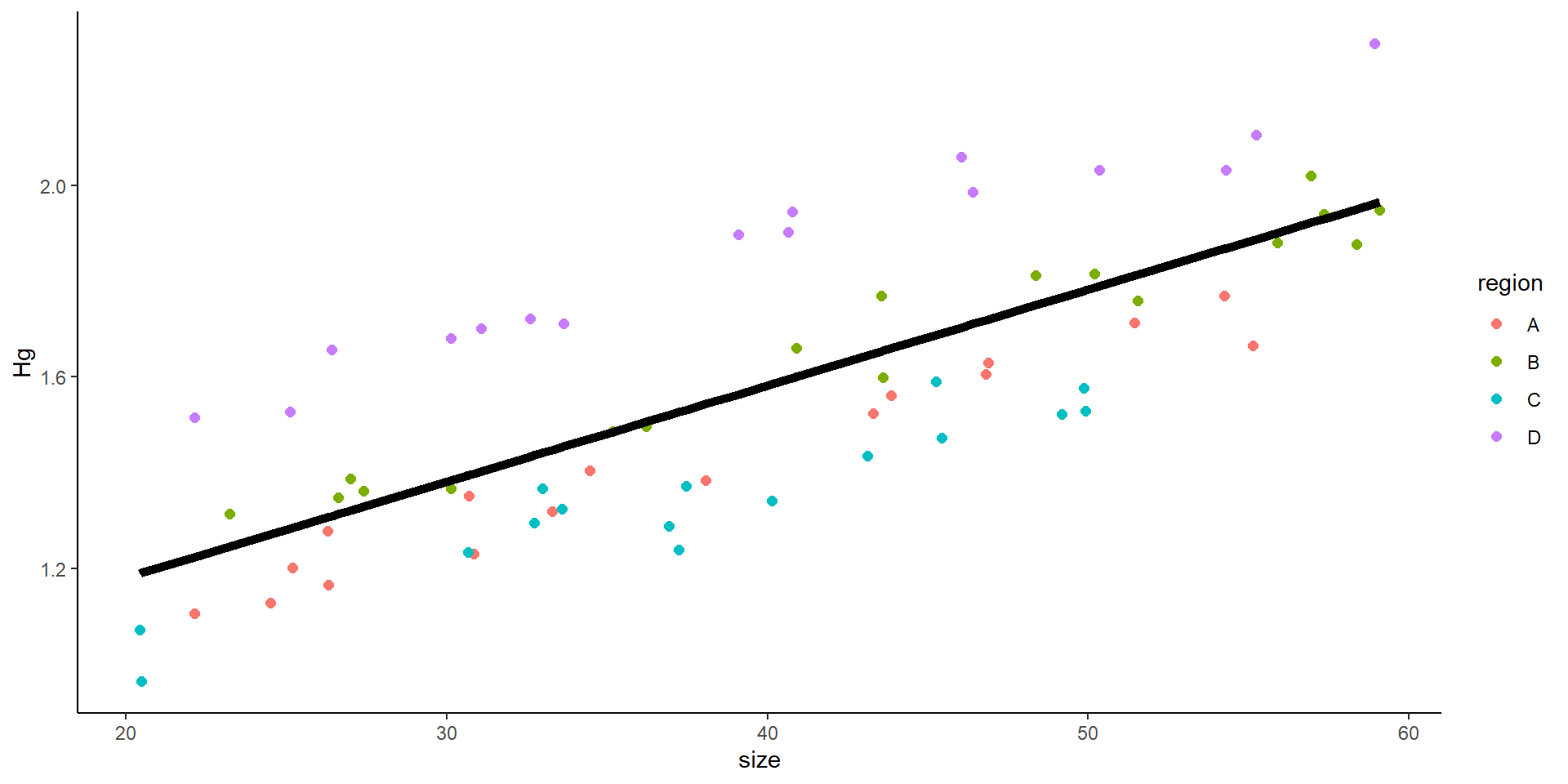
The variance can affect the slope, the intercept, or both

  • Random effects introduce variance.

  • It can introduce variance to the intercept or to the slope

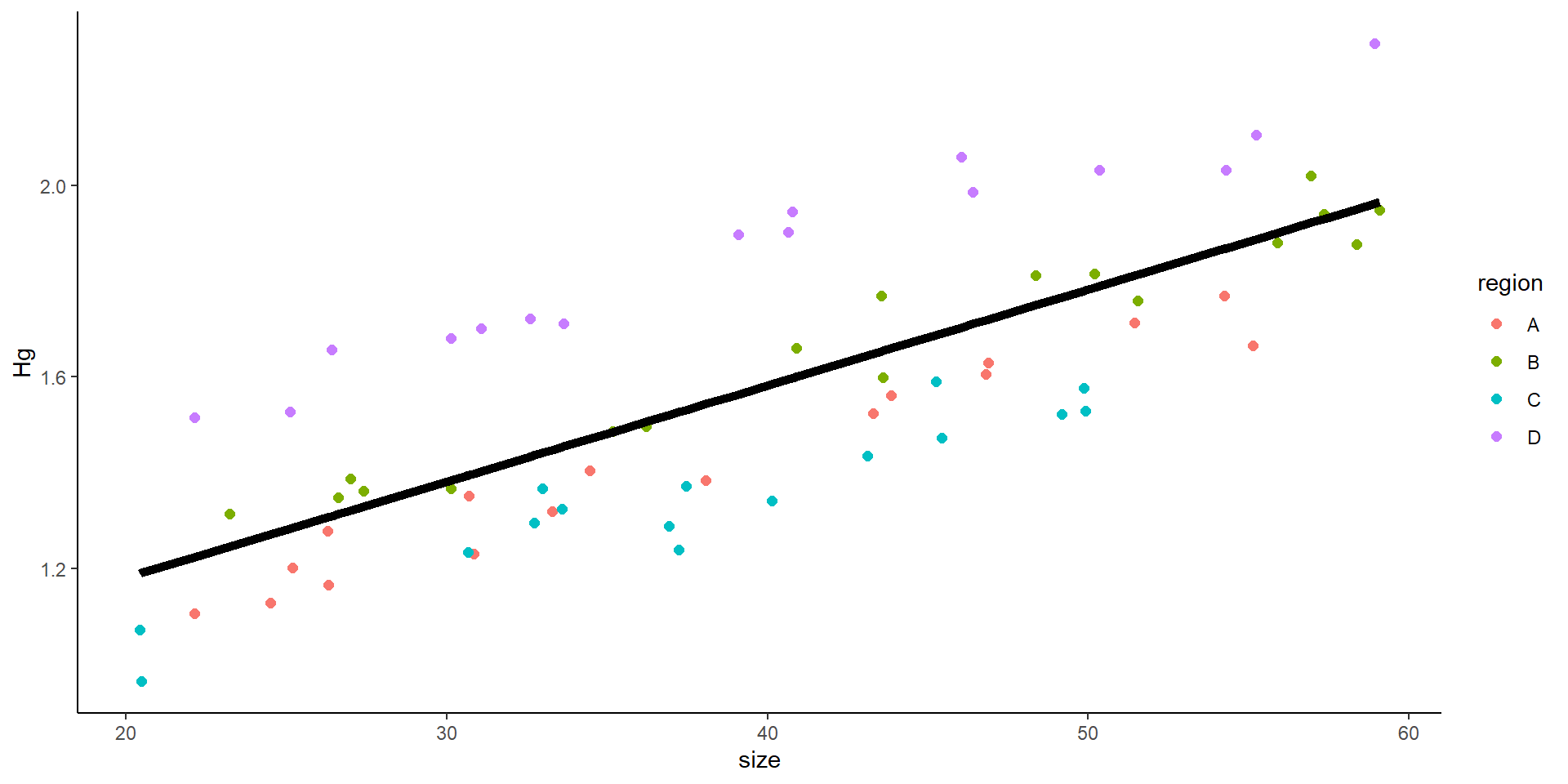
Mixed model

  • No mixed model:

  • \[ Hg_i \sim \beta_0 + \beta_1size_{i} + \epsilon_i \]

  • What is i?

  • We have two sources of variance (error): The fish (i) and the net (j)

  • i individuals, j sites (4)

Mixed model

No mixed model:

\[Hg_i \sim \beta_0 + \beta_1size_{i} + \epsilon_i \]

  • Mixed model: i individuals and j sites introduced as error.

  • We can do a mixed model with mixed intercept or mixed slope

  • mixed intercept (nets only affect the intercept) –> analogous to additive model:

  • \[ Hg_{ij} \sim \underbrace{(\beta_0 +\underbrace{\gamma_j}_{\text{Random intercept}})}_{intercept} + \underbrace{\beta_1size_{i}}_{slope} +\underbrace{\epsilon_i}_\text{ind var} \]

  • Variance comes from random “selection” of fish within a net

  • \(\epsilon_i \sim N(0, \sigma)\)

  • Variance comes from random “selection” of sites

  • \(\gamma_j \sim N(0,\sigma_j)\)

  • What does a mixed intercept mean?

Mixed model with random intercept

This is the result of a mixed model:

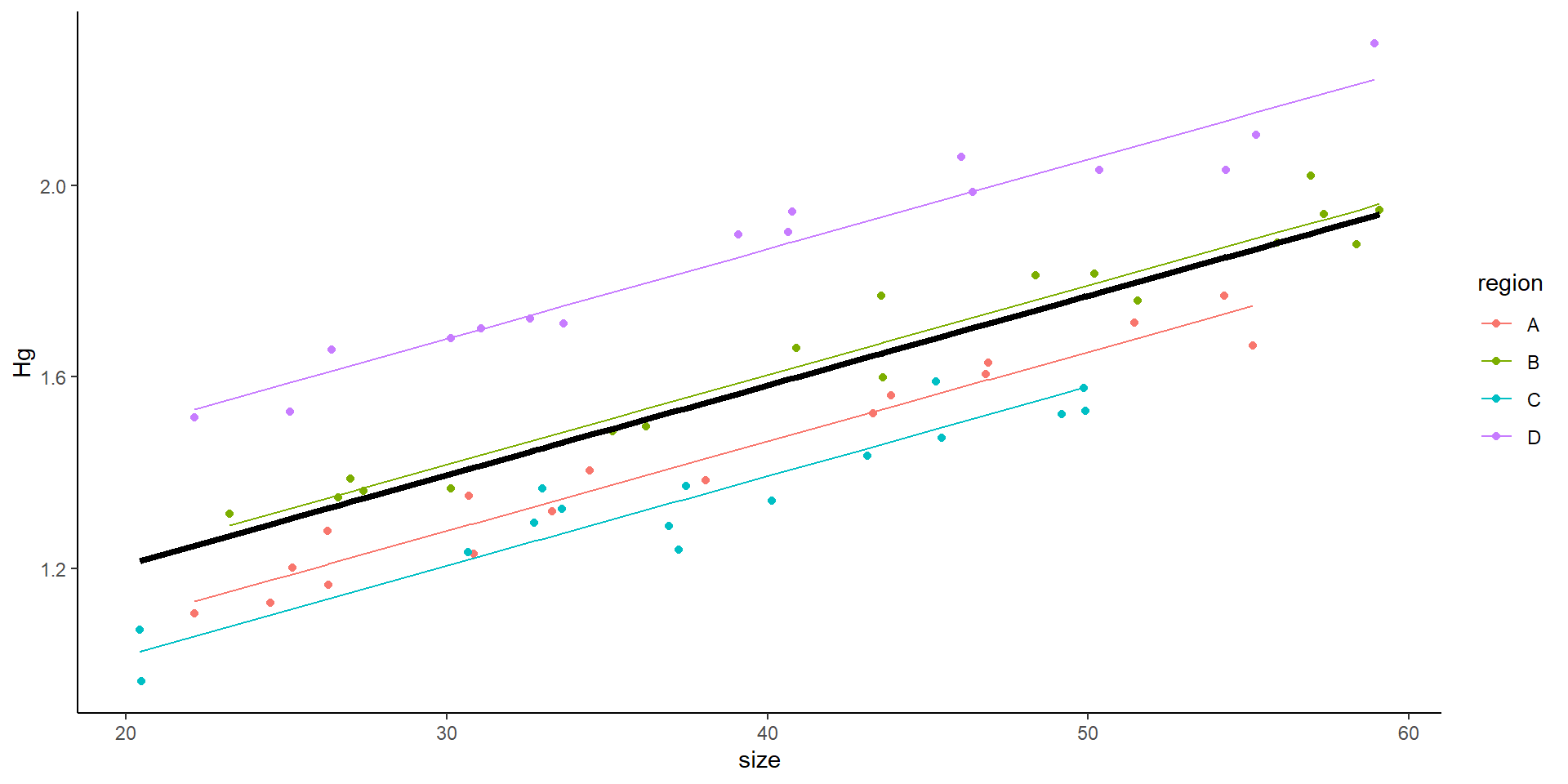
  • What does the random intercept mean?
  • Why not simply do:
  • \(Hg_i \sim \beta_0 + \beta_1size_{i} + \beta_2rB_{i} + \beta_3rC_{i} + \beta_4rD_{i}+ \epsilon_i\)
  • Model with effect of site

Mixed model with random intercept

 Family: gaussian  ( identity )
Formula:          Hg ~ size + (1 | region)
Data: HgDat_df

     AIC      BIC   logLik deviance df.resid 
  -177.1   -168.3     92.6   -185.1       63 

Random effects:

Conditional model:
 Groups   Name        Variance Std.Dev.
 region   (Intercept) 0.032847 0.18124 
 Residual             0.002688 0.05184 
Number of obs: 67, groups:  region, 4

Dispersion estimate for gaussian family (sigma^2): 0.00269 

Conditional model:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) 0.8357038  0.0937058    8.92   <2e-16 ***
size        0.0186742  0.0005839   31.98   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

\[ Hg_{ij} = \underbrace{(\beta_0 +\underbrace{\gamma_j}_{\text{Random intercept}})}_{intercept} + \underbrace{\beta_1size_{i}}_{slope} +\underbrace{\epsilon_i}_\text{ind var} \]

  • Where:

  • \[ \epsilon_i \sim N(0,\sigma^2) \]

  • \[ \gamma_j \sim N(0,\sigma^2_\gamma) \]

Mixed effects models: how to run them?

library(glmmTMB)
m2<- glmmTMB(Hg~size +(1|region), data=HgDat_df)

  • Random effects are specified as \(x|g\)

  • x is an effect

  • g is grouping factor (categorical)

  • \(1|region\)

  • Effect -> 1 (intercept)
    Grouping factor -> region

Mixed effects model output

 Family: gaussian  ( identity )
Formula:          Hg ~ size + (1 | region)
Data: HgDat_df

     AIC      BIC   logLik deviance df.resid 
  -177.1   -168.3     92.6   -185.1       63 

Random effects:

Conditional model:
 Groups   Name        Variance Std.Dev.
 region   (Intercept) 0.032847 0.18124 
 Residual             0.002688 0.05184 
Number of obs: 67, groups:  region, 4

Dispersion estimate for gaussian family (sigma^2): 0.00269 

Conditional model:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) 0.8357038  0.0937058    8.92   <2e-16 ***
size        0.0186742  0.0005839   31.98   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1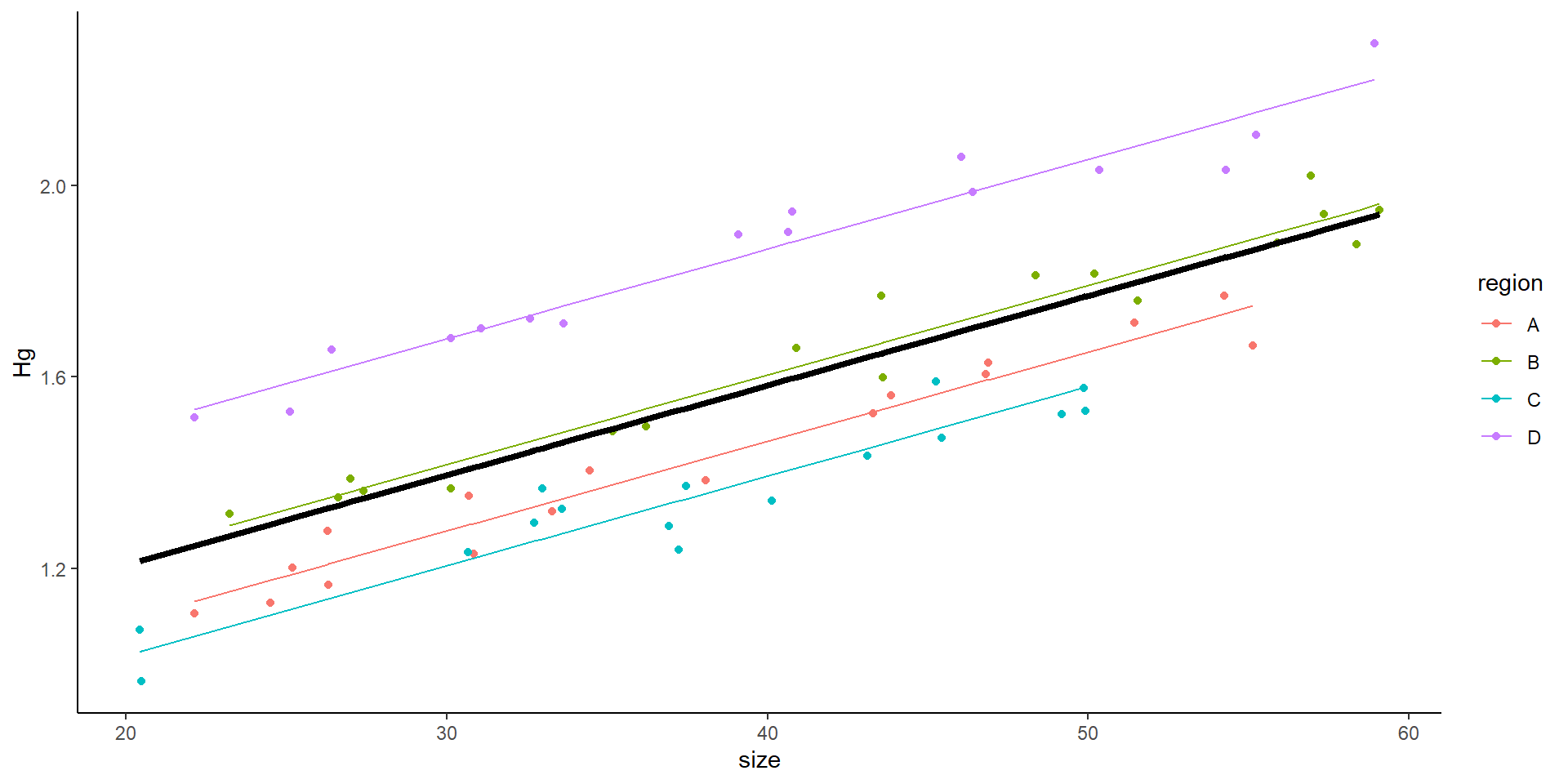

Mixed model with random intercept and random slope

  • \[ Hg_i \sim \beta_0 + \beta_1size_{i} + \epsilon_i \]

  • i individuals, j sites (4)

  • \[ Hg_{ij} \sim \underbrace{(\beta_0 +\underbrace{\gamma_j}_{\text{Random intercept}})}_{intercept} + \underbrace{(\beta_1+\underbrace{\psi_j}_{\text{Random slope}})size_{i}}_{slope} +\underbrace{\epsilon_i}_\text{ind var} \]

  • Variance comes from random “selection” of fish within a net

  • Variance comes from random “selection” of sites

  • Where,

  • \[ \epsilon_i \sim N(0,\sigma^2) \]

  • \[ \gamma_j \sim N(0,\sigma^2_\gamma) \]

  • \[ \psi_j \sim N(0,\sigma^2_\psi) \]

Random slope and intercept

m3<-glmmTMB(Hg~size +(1+size|region), data=HgDat2_df)
summary(m3)
 Family: gaussian  ( identity )
Formula:          Hg ~ size + (1 + size | region)
Data: HgDat2_df

     AIC      BIC   logLik deviance df.resid 
  -153.4   -138.4     82.7   -165.4       83 

Random effects:

Conditional model:
 Groups   Name        Variance  Std.Dev. Corr 
 region   (Intercept) 2.765e-02 0.166290      
          size        8.865e-05 0.009415 0.30 
 Residual             6.287e-03 0.079291      
Number of obs: 89, groups:  region, 4

Dispersion estimate for gaussian family (sigma^2): 0.00629 

Conditional model:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) 1.157873   0.089296  12.967  < 2e-16 ***
size        0.034451   0.004772   7.219 5.23e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

  • Random effects are specified as \(x|g\)

  • x is an effect

  • g is grouping factor (categorical)

  • \(1 + size|region\)

  • Effect -> 1 (intercept) + size
    Grouping factor -> region

Random slope and intercept

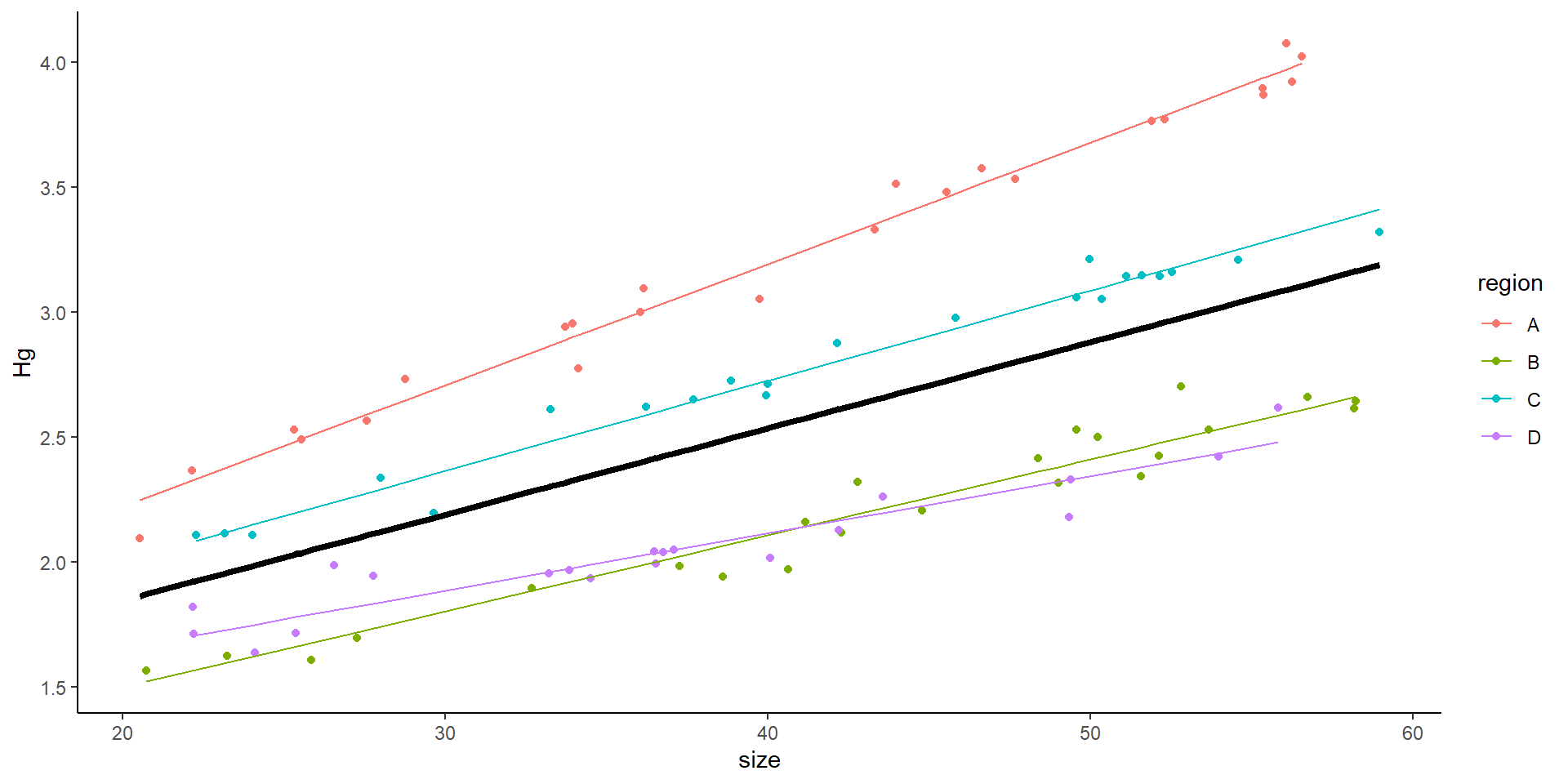
Only random slope

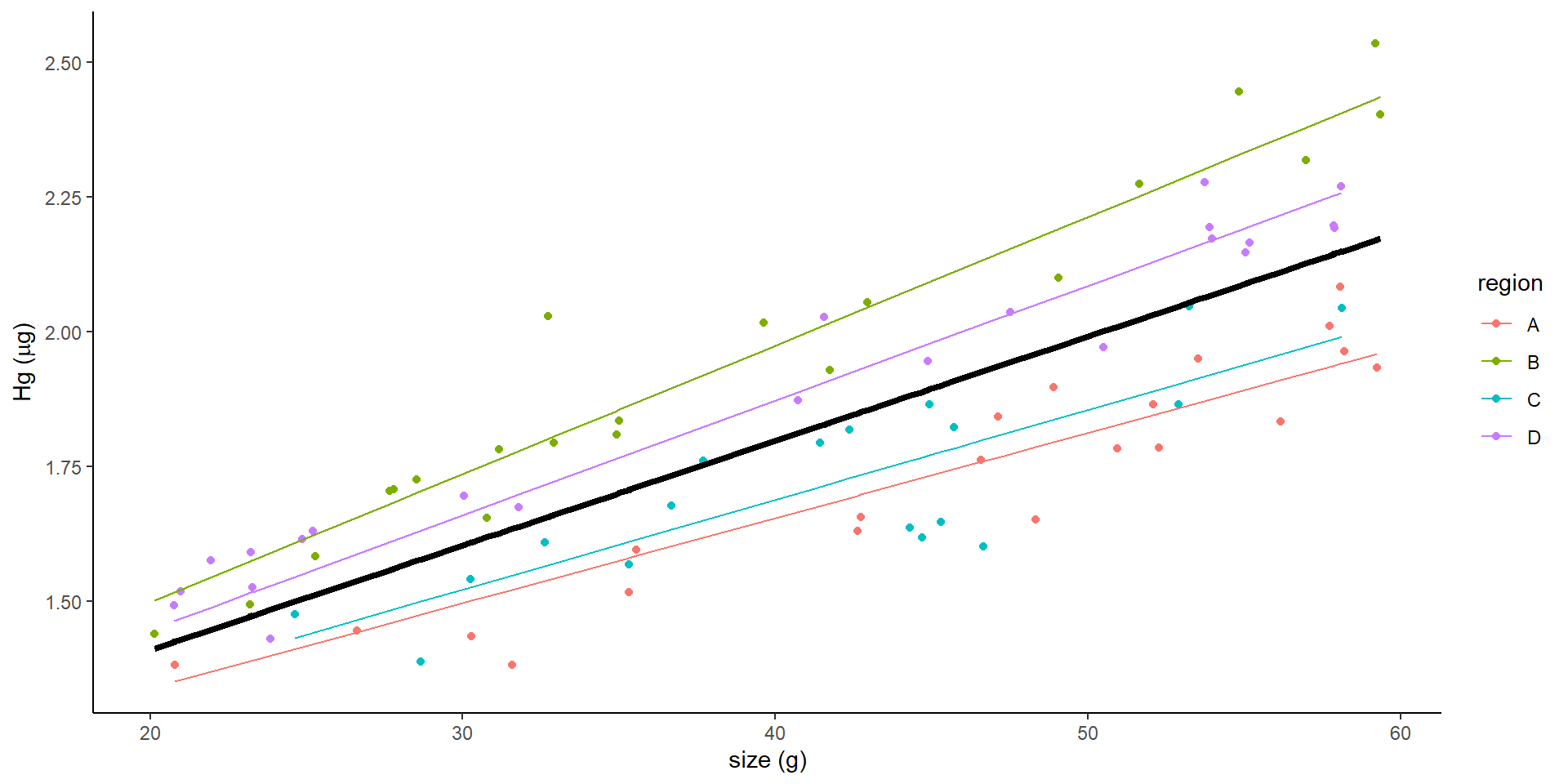
 Family: gaussian  ( identity )
Formula:          Hg ~ size + (0 + size | region)
Data: HgDat2_df

     AIC      BIC   logLik deviance df.resid 
  -158.4   -148.8     83.2   -166.4       79 

Random effects:

Conditional model:
 Groups   Name Variance  Std.Dev.
 region   size 1.103e-05 0.003321
 Residual      6.441e-03 0.080256
Number of obs: 83, groups:  region, 4

Dispersion estimate for gaussian family (sigma^2): 0.00644 

Conditional model:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) 1.021430   0.031578   32.35   <2e-16 ***
size        0.019400   0.001817   10.68   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We don’t do this

  • \(E(Hg_i) = \beta_0 + \beta_1*size_{i}\)

  • Pseudoreplication

  • \(E(Hg_i) = \beta_0 + \beta_1size_{i} + \beta_2 site2_i + \beta_3 site3_i + \beta_4 site4_i\)

  • We don’t care about the specific sites… we want whole population-wide!

What do we want to know?

  • Mercury concentration population-wide

  • Variance introduces by placement of the nets

  • \[ Hg_{ij} \sim \underbrace{(\beta_0 +\underbrace{\gamma_j}_{\text{Random intercept}})}_{intercept} + \underbrace{(\beta_1+\underbrace{\psi_j}_{\text{Random slope}})size_{i}}_{slope} +\underbrace{\epsilon}_\text{ind var} \]

  • \(\gamma_j \sim Normal(0,\sigma_\gamma)\)

  • \(\psi_j \sim Normal(0,\sigma_\psi)\)

  • \(\epsilon \sim Normal(0,\sigma)\)

GLM’s

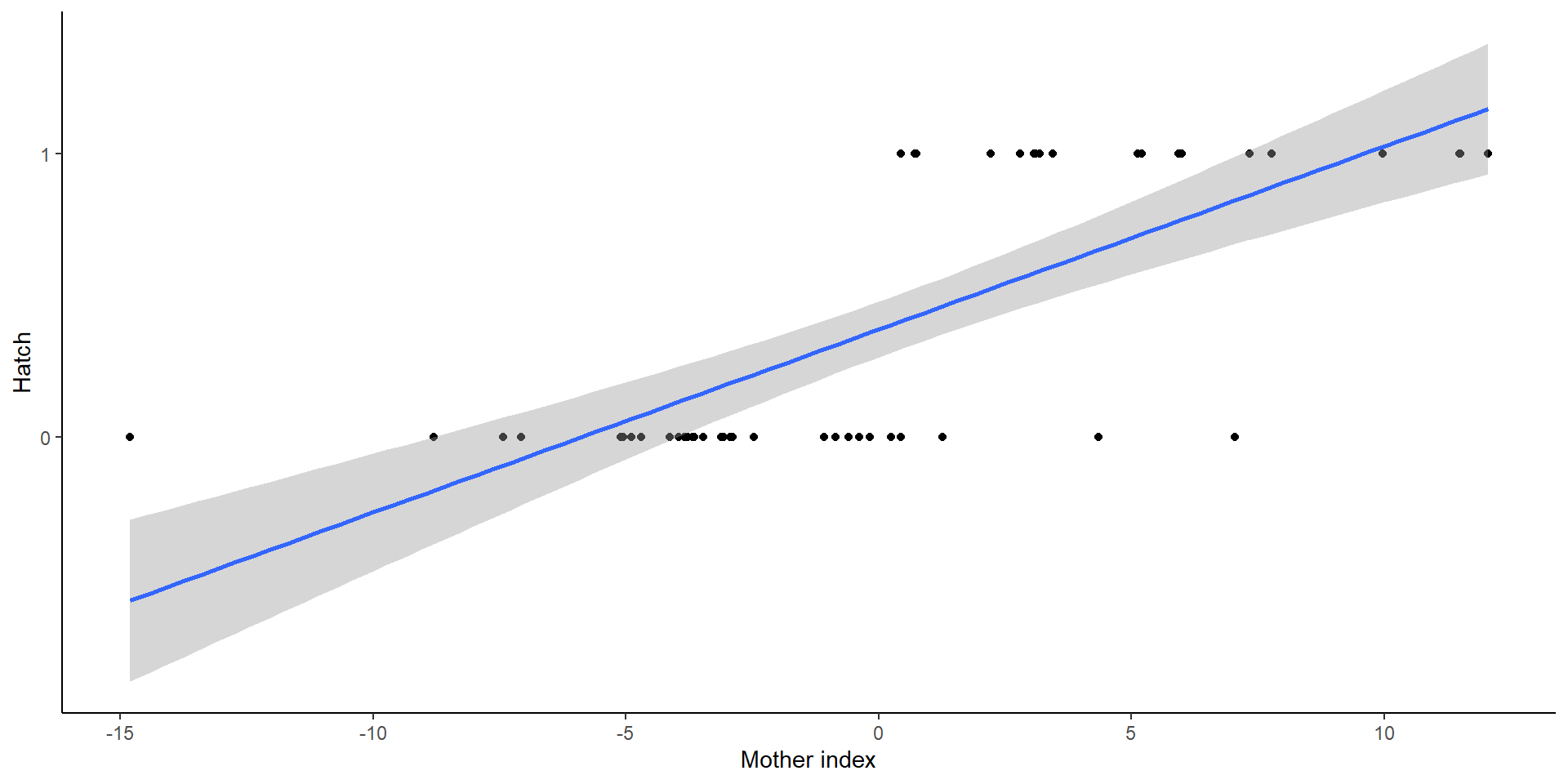
  • How many assumptions does it break?

Glm’s

What do Glm’s do?

  1. Transform the response to linear
  2. Have a different distribution of the residuals

If normal:

  • \[ \underbrace{E[y_i]}_{\text{expected value}} = \underbrace{\beta_0 + \beta_1x_{1,i} + ... \beta_mx_{m,i}}_{deterministic} \]

  • \[ y_i \sim \underbrace{N(mean=E[y_i], var=\sigma^2)}_{stochastic} \]

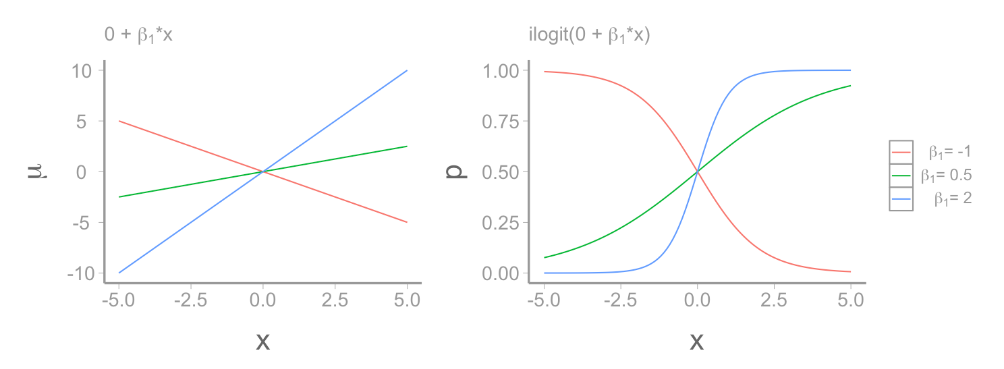
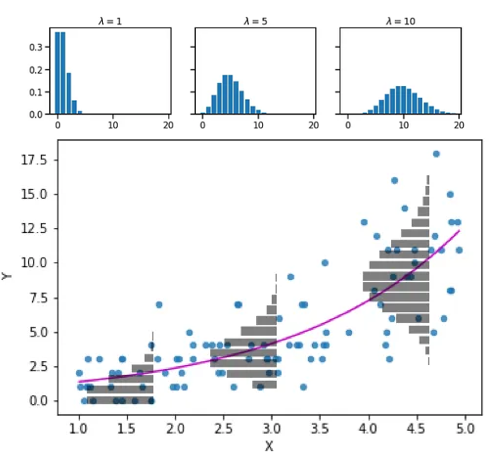
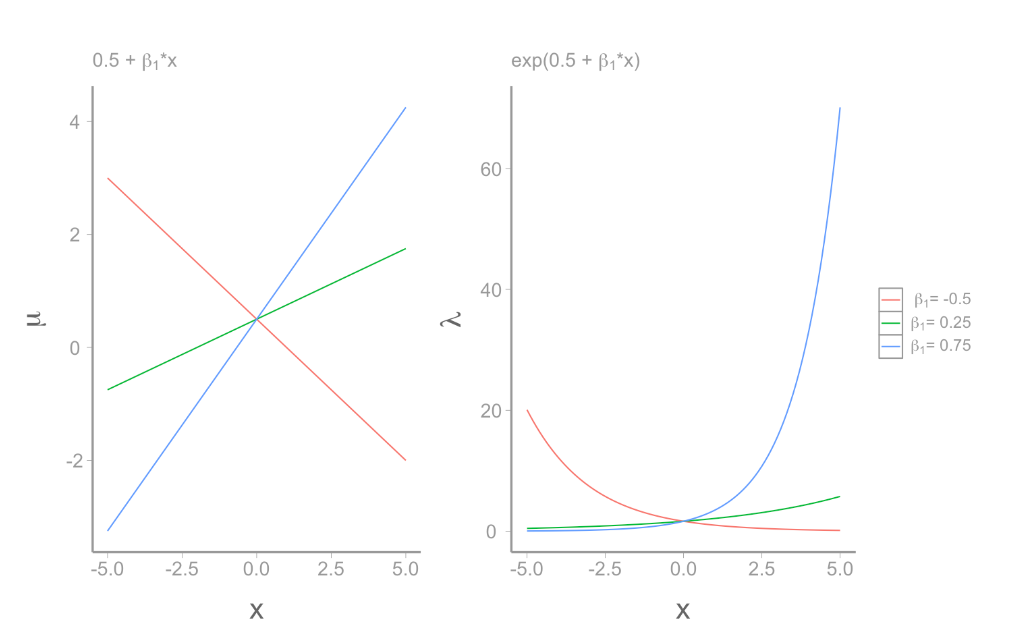
  • Poisson glm:

  • \[ \underbrace{log(\lambda)}_{\text{link function}} = \underbrace{\beta_0 + \beta_1x_{1,i} + ... \beta_mx_{m,i}}_{deterministic} \]

    \[ y_i \sim \underbrace{Poisson(\lambda)}_{stochastic} \]

  • Negative Binomial glm:

  • \[ \underbrace{log(\lambda)}_{\text{link function}} = \underbrace{\beta_0 + \beta_1x_{1,i} + ... \beta_mx_{m,i}}_{deterministic} \]

    \[ y_i \sim \underbrace{NB(\mu,\theta)}_{stochastic} \]

  • \(variance = \frac{\theta}{\mu+\theta}\)

GLM’s

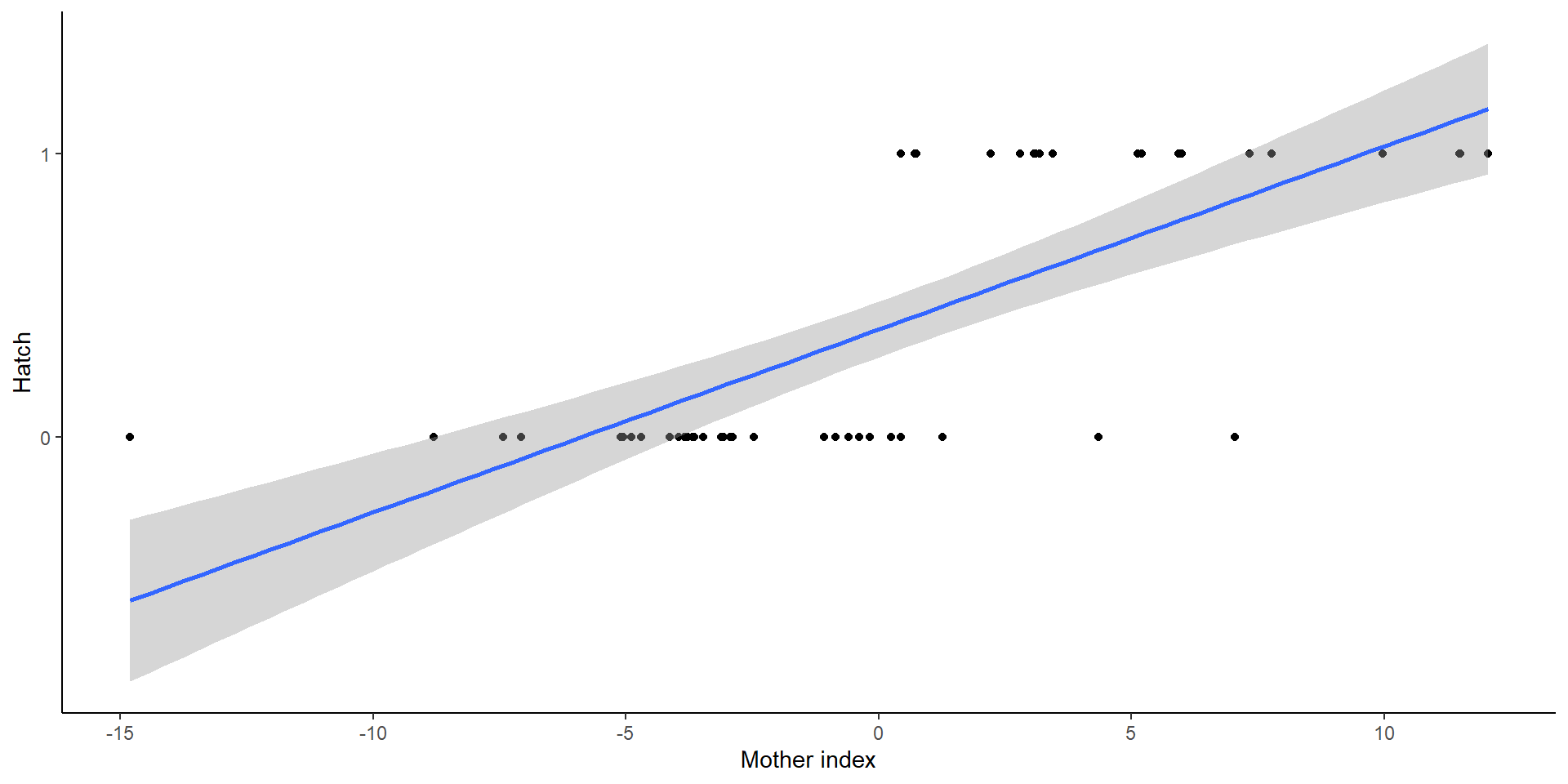
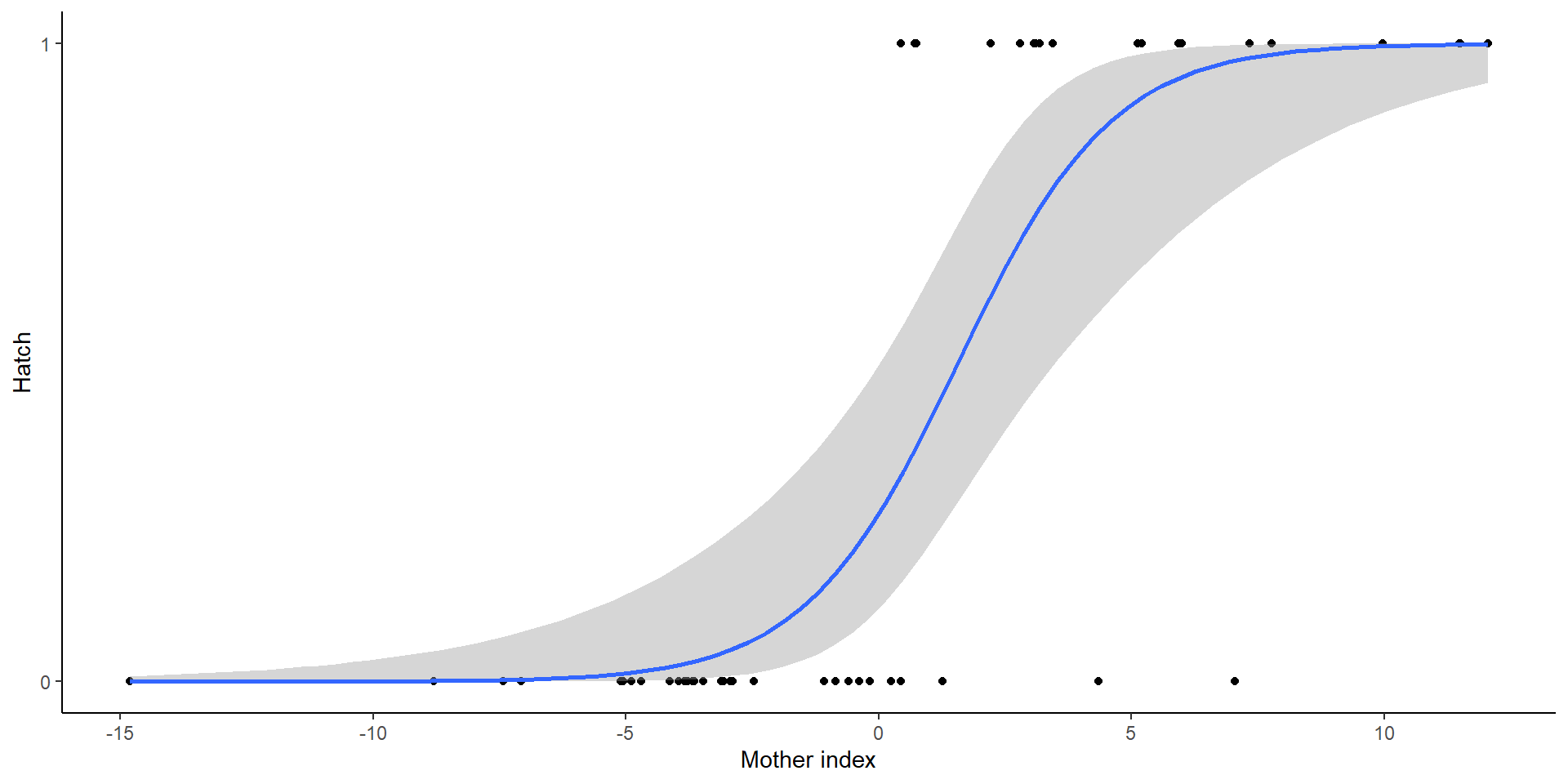
GLM’s

GLM’s

GLM’s

Mixed models

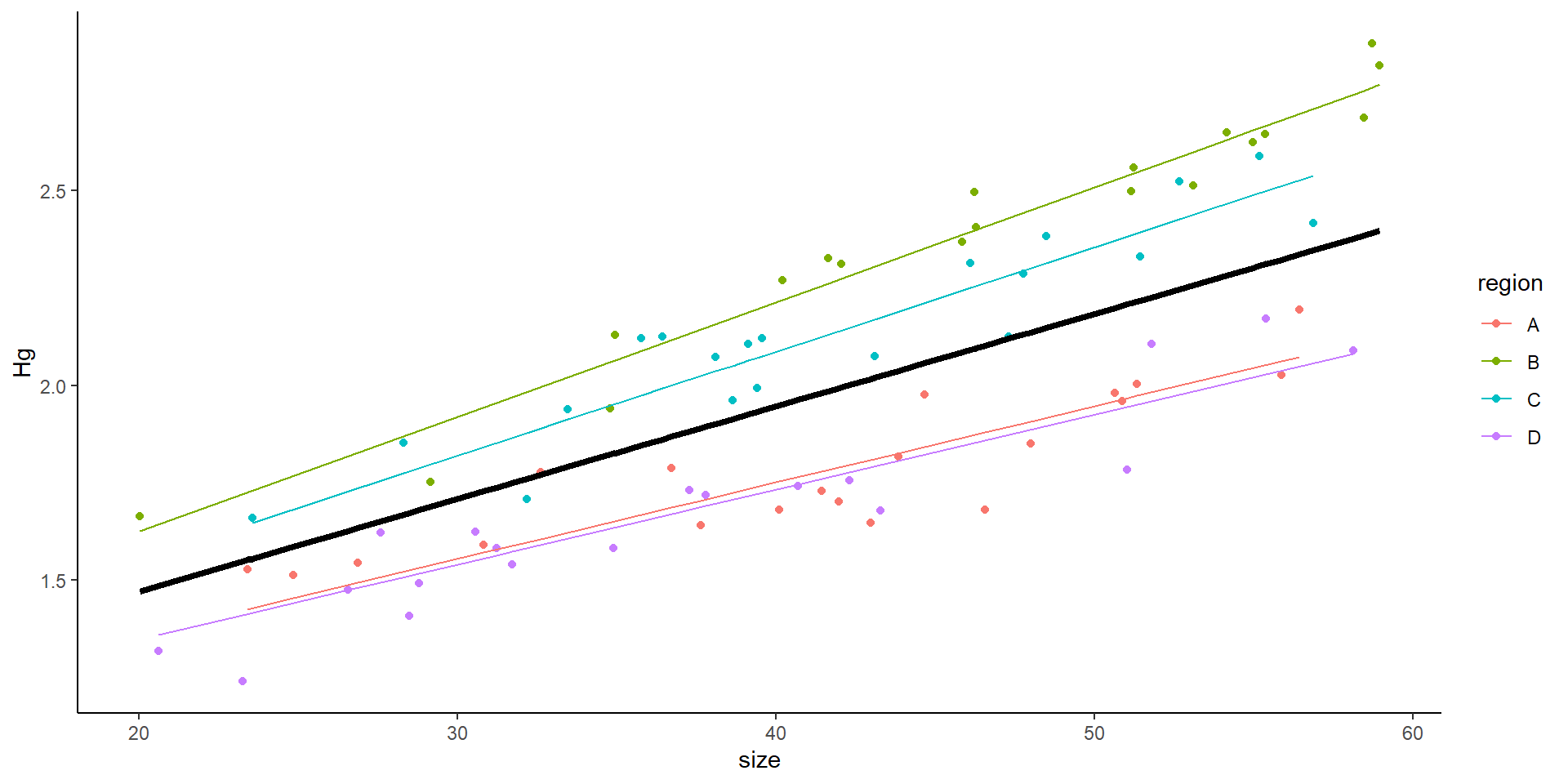
If we set all random effects to zero, we get population mean, and predicted value for a random individual

Mixed effects

Set nets on each of those sites

  • Measure 50, 43, 67, and 90 fish. For number of parasites OR presence of parasites?

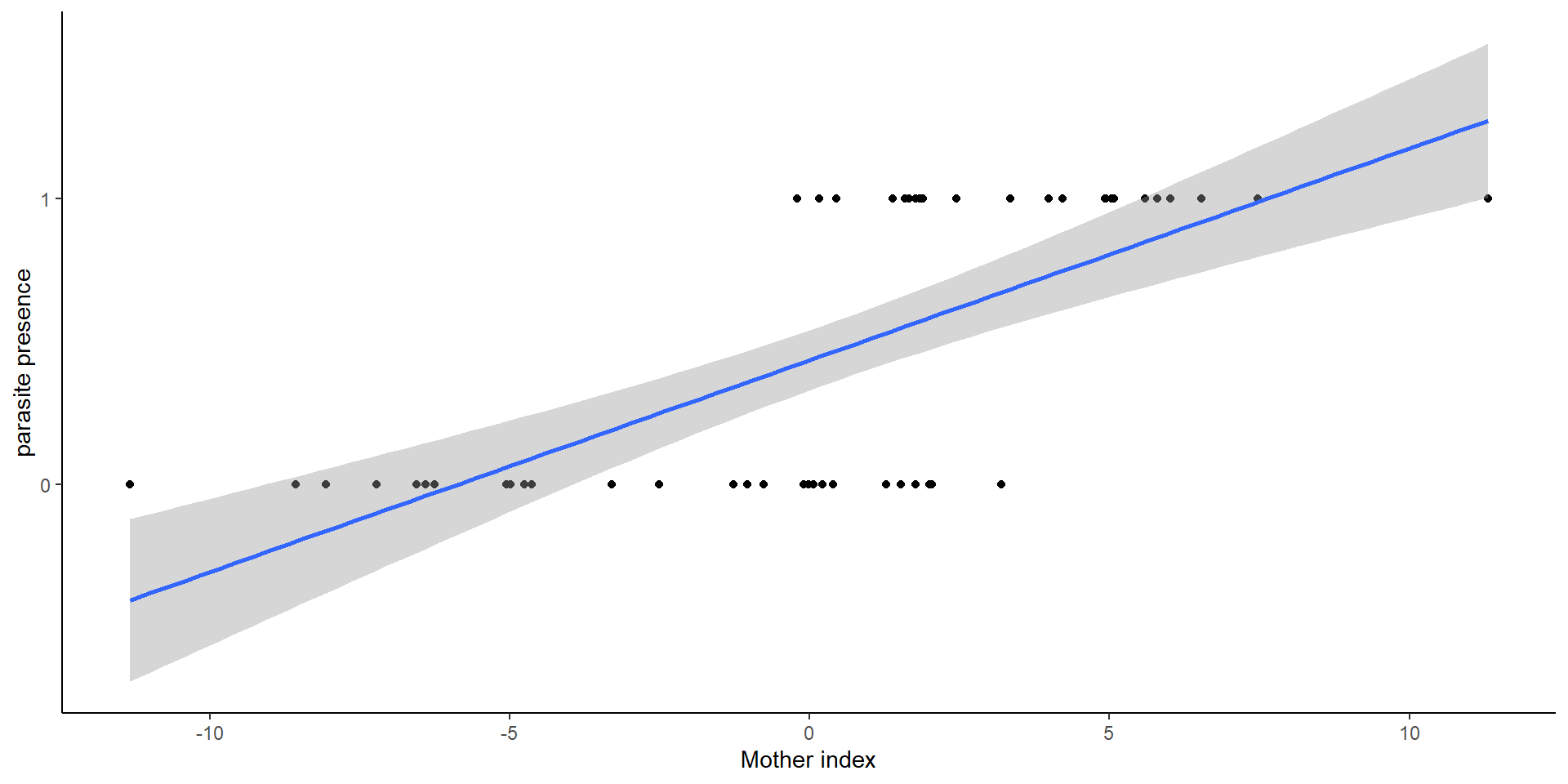
Generalized linear mixed effects models

  • Linear portion of the Mixed effects models have a deterministic and stochastic component

  • Count data

  • Binary data (1, 0)

GLMM’s

  • How can we run mixed effects models?

  • Easy way: Add random effects to the linear predictor, leading to generalized linear mixed effect models

  • Essentially, you have two sources of variation

  • One is normally dsitributed, the other one is distributed according to a different distribution

Example

A poisson glm:

  • \(log(\lambda) = \beta_0 + \beta_1x_i\)

  • \(y_i \sim Poisson(\lambda)\)

  • A glmm: Poisson-normal

  • \(log(\lambda) = (\beta_0+\gamma) + (\beta_1+\psi)x_{ij}\)

  • \(\gamma \sim N(0,\sigma_\gamma)\) , \(\psi\sim N(0,\sigma_\psi)\)

  • \(y_i \sim Poisson(\lambda)\)

Parameter interpretation

  • Not easy to interpret!

  • In random effects if we set all random effects to 0, then we estimate the mean for a “typical” individual

  • “typical means subject, site, individual, etc.”

  • The variances are in different distributions

  • Typical individual does not equal “population average response”

Example

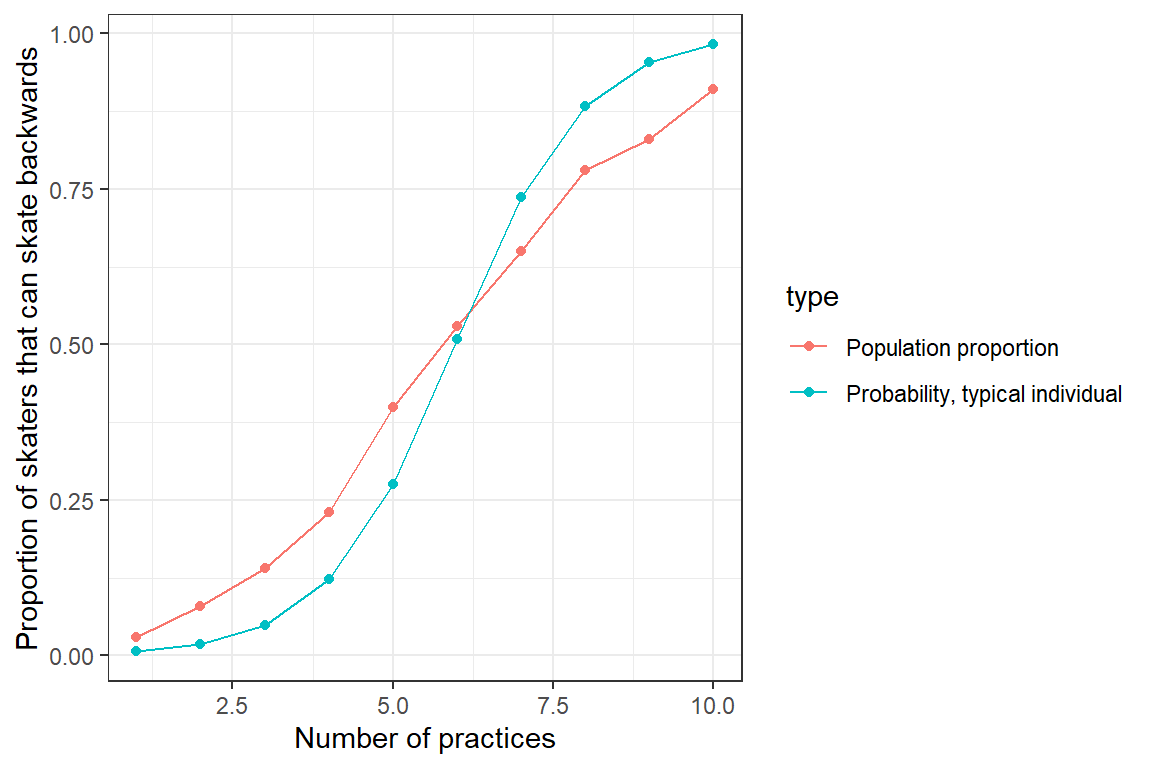
Both curves are not lining up

  • Due to non-logit transformations (random effects are normal)

Interpreting data

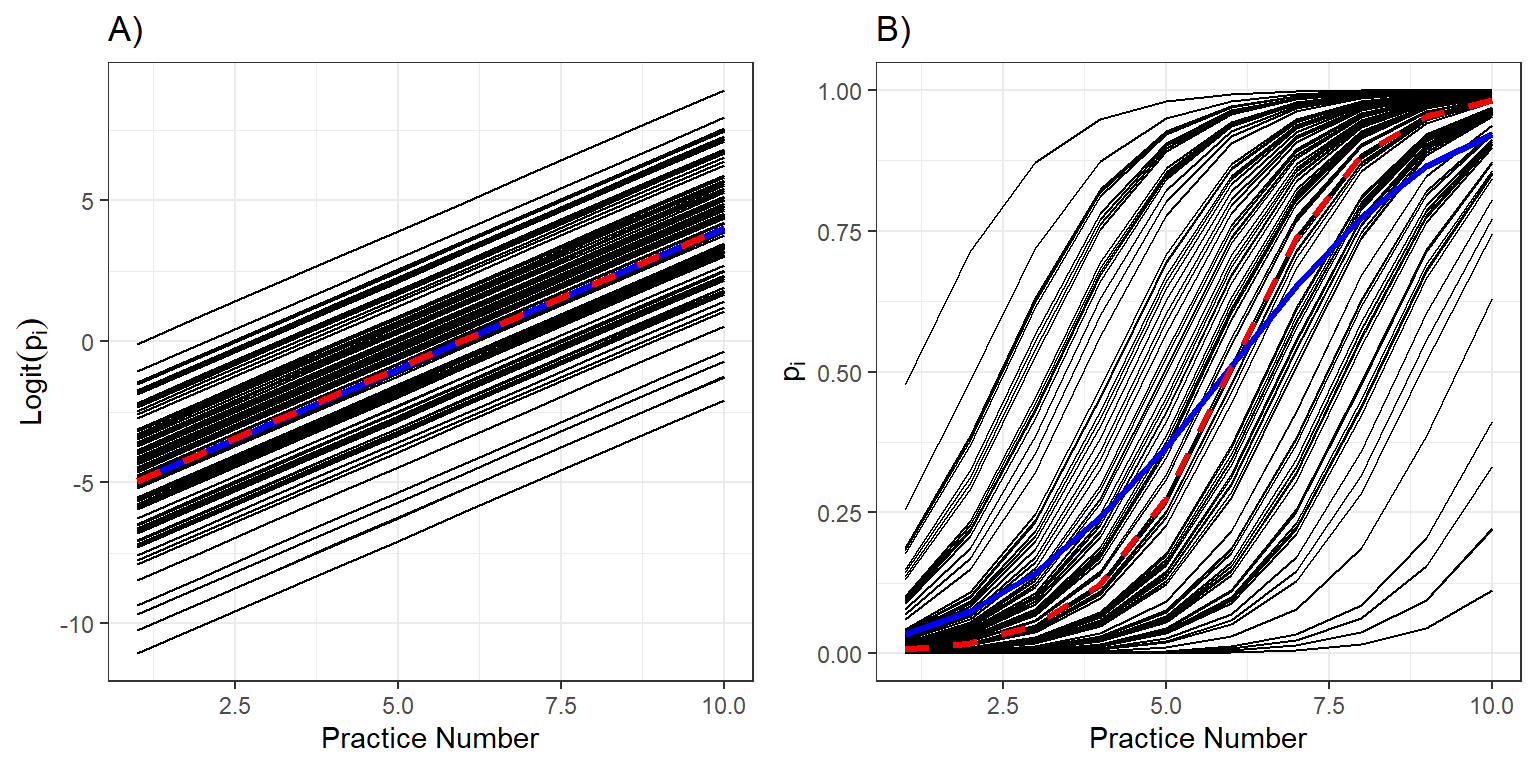
  • Individual response curves (black), the response curve for a typical individual with random effects at zeroes, and the population mean response curve (blue) and on the logit and probability scales

In other words

  • A glmm: Poisson-normal

  • \(log(\lambda) = (\beta_0+\gamma) + (\beta_1+\psi)x_{ij}\)

  • \(\gamma \sim N(0,\sigma_\gamma)\) , \(\psi\sim N(0,\sigma_\psi)\)

  • \(y_i \sim Poisson(\lambda)\)

  • Because of non linearity if we set \(\gamma\) and \(\psi\) to 0’s, the end result will be different than if we get the mean of the overall response

Take away

If you do glmm’s be very careful about interpretation

  • In general, transforming data can be risky

Solutions?

  • Package GLMMadaptive estimates marginal means

  • How can we run mixed effects models?

  • Easy way: Add random effects to the linear predictor, leading to generalized linear mixed effect models

  • Hard way: Generalized Estimating Equations

  • https://fw8051statistics4ecologists.netlify.app/gee

Example

  1. Zuur, A., Ieno, E. N., Walker, N., Saveliev, A. A. & Smith, G. M. Mixed Effects Models and Extensions in Ecology with R. (Springer New York, 2009).

https://www.highstat.com/

RIKZ data

RIKZ data

  • RIKZ institute

  • Inter-tidal area (AKA beach): 9

  • In each beach, 5 samples were taken

  • Response variable: macro-fauna richness (AKA number of species)

  • NAP: height of sampling station compared to mean tidal level

  • Exposure (index). Of multiple environmental conditions. Treated as categorical, as there are three levels

RIKZ data

flowchart TD

  A[RIKZ DATA] --> B(Beach 1)
  A --> C(Beach 2)
  A --> E(Beach 9)
  B --> F(site 1)
  B --> G(site 2)
  B --> H(site 3)
  B --> I(site 4)
  B --> J(site 5)
  C --> K(site 1)
  C --> L(site 2)
  C --> M(site 3)
  C --> N(site 4)
  C --> O(site 5)
  E --> P(site 1)
  E --> Q(site 2)
  E --> R(site 3)
  E --> S(site 4)
  E --> T(site 5)

Let’s work on this example

Objective

flowchart TD

  A[RIKZ DATA] --> B(Beach 1)
  A --> C(Beach 2)
  A --> E(Beach 9)
  B --> F(site 1)
  B --> G(site 2)
  B --> H(site 3)
  B --> I(site 4)
  B --> J(site 5)
  C --> K(site 1)
  C --> L(site 2)
  C --> M(site 3)
  C --> N(site 4)
  C --> O(site 5)
  E --> P(site 1)
  E --> Q(site 2)
  E --> R(site 3)
  E --> S(site 4)
  E --> T(site 5)

  • Exploring whether there is a relationship between richness and the two factors: NAP and exposure

  • We have an N of 45… but do we?

  • We have multiple potential alternatives: there is an effect of NAP, an effect of Exposure, an effect of both, of neither

  • Also… there are mixed effects

  • Random intercept, random slope, both? –> let’s wait to discuss this

  • Step 1: Read the data… there is a potential issue

rikz<-read.table(file = "RIKZ.txt", header = TRUE, dec = ",")
str(rikz)
  • Step 2: decide our analysis! 🤔 Any ideas? any details?

The data

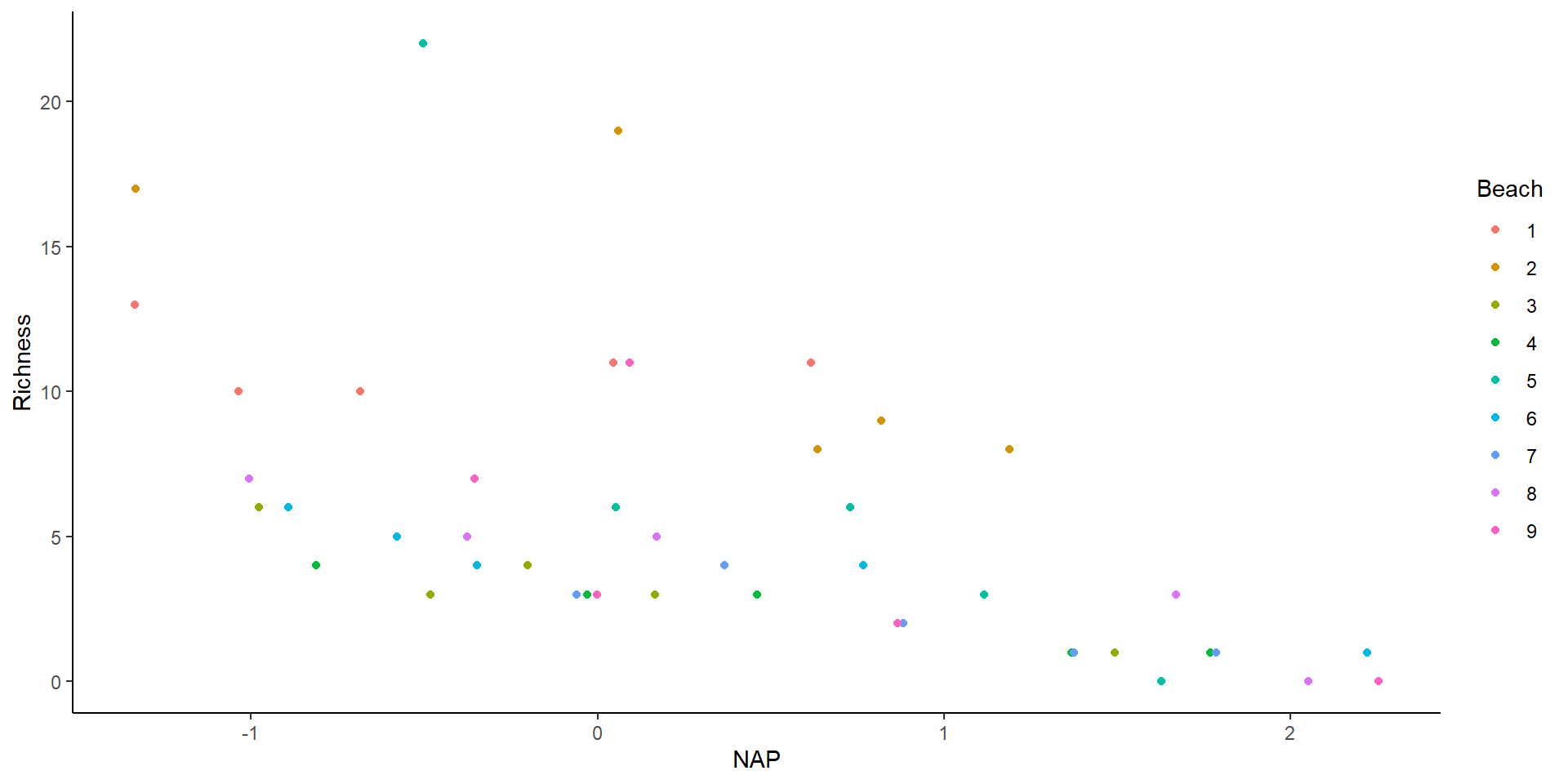
The data

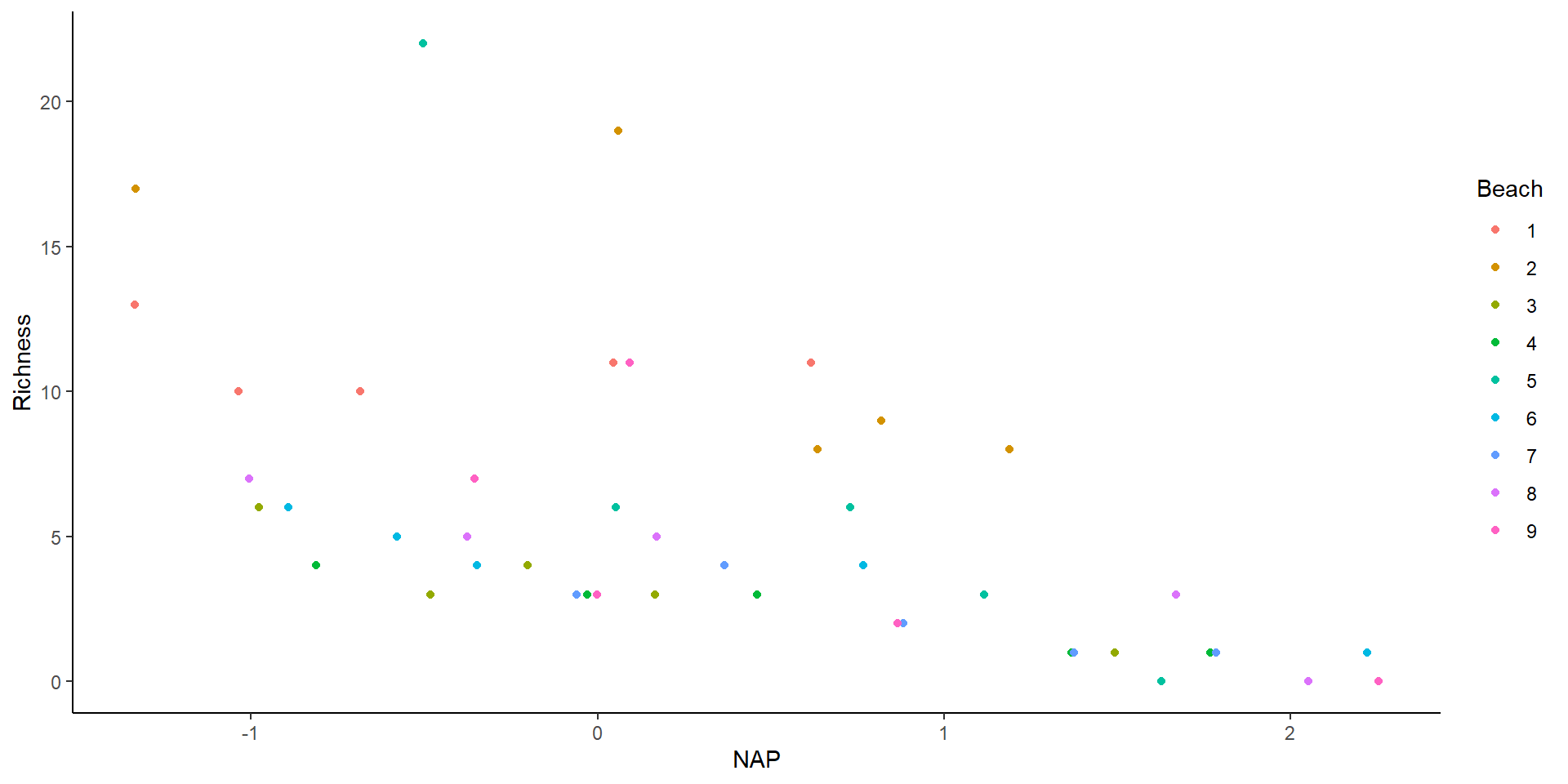
  • There seems to be an effect of NAP…

  • how about… a random effect of beach?

  • step 3: how do we decide random effects?

  • step 3: random intercept? Or random slope? Or both? Or non

  • What do we do?

  • Exposure is categorical… so no random slope 😃

Model selection with random models

WE CANNOT TEST FIXED AND RANDOM EFFECTS AT THE SAME TIME

  • Test randomeffects first.

  • We use the “global” or saturated fixed model

  • How many models?

  • Use AIC

  • What model structure?

Model selection with random models

Four models. Run all with glmmTMB

Step 1: install the glmmTMB package

Model selection with random models

Fixed effects: NAP*Exposure

Family: Poisson


Model selection based on AICc:

     K   AICc Delta_AICc AICcWt Cum.Wt     LL
Mod1 6 210.94       0.00   0.62   0.62 -98.36
Mod3 7 213.24       2.30   0.20   0.81 -98.10
Mod2 7 213.52       2.59   0.17   0.98 -98.25
Mod4 9 217.81       6.87   0.02   1.00 -97.33

Are the AIC values the same?

Notes on AIC

I recommend using the AICcmodavg package and making a list!

library(AICcmodavg)
aictab(list(model1,model2,model3,model4))

Next step: let’s explore the model (factors!)

How do you explore the best model?

Let’s look at the summary

Analysis of Deviance Table (Type II Wald chisquare tests)

Response: Richness
               Chisq Df Pr(>Chisq)    
NAP          51.7328  1  6.359e-13 ***
Exposure     55.4525  2  9.092e-13 ***
NAP:Exposure  3.5604  2     0.1686    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Next step: let’s explore the model (factors!)

Anova(model1)
Analysis of Deviance Table (Type II Wald chisquare tests)

Response: Richness
               Chisq Df Pr(>Chisq)    
NAP          51.7328  1  6.359e-13 ***
Exposure     55.4525  2  9.092e-13 ***
NAP:Exposure  3.5604  2     0.1686    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • Talk about Zuur’s approach here

Next step?

model1<-glm(Richness~NAP*Exposure, data = rikz, family = poisson)
model2<-glm(Richness~NAP+Exposure, data = rikz, family = poisson)
model3<-glm(Richness~NAP, data = rikz, family = poisson)
model4<-glm(Richness~Exposure, data = rikz, family = poisson)
model5<-glm(Richness~1, data = rikz, family = poisson)

modeltab<-AICcmodavg::aictab(list(model1,model2,model3,model4,model5))
modeltab

Model selection based on AICc:

     K   AICc Delta_AICc AICcWt Cum.Wt      LL
Mod2 4 209.37       0.00   0.69   0.69 -100.19
Mod1 6 210.94       1.57   0.31   1.00  -98.36
Mod3 2 259.47      50.10   0.00   1.00 -127.59
Mod4 3 265.87      56.50   0.00   1.00 -129.64
Mod5 1 323.84     114.47   0.00   1.00 -160.88

Evidence ratios

Burnham and Anderson

Evidence ratios


Evidence ratio between models 'Mod2' and 'Mod1':
2.19
  • Raffle tickets

Last step: Model validation

Of the best model.

Other steps?

Check assumptions (if normal)