Bayesian statistics: part two

SNR 610

Bayesian

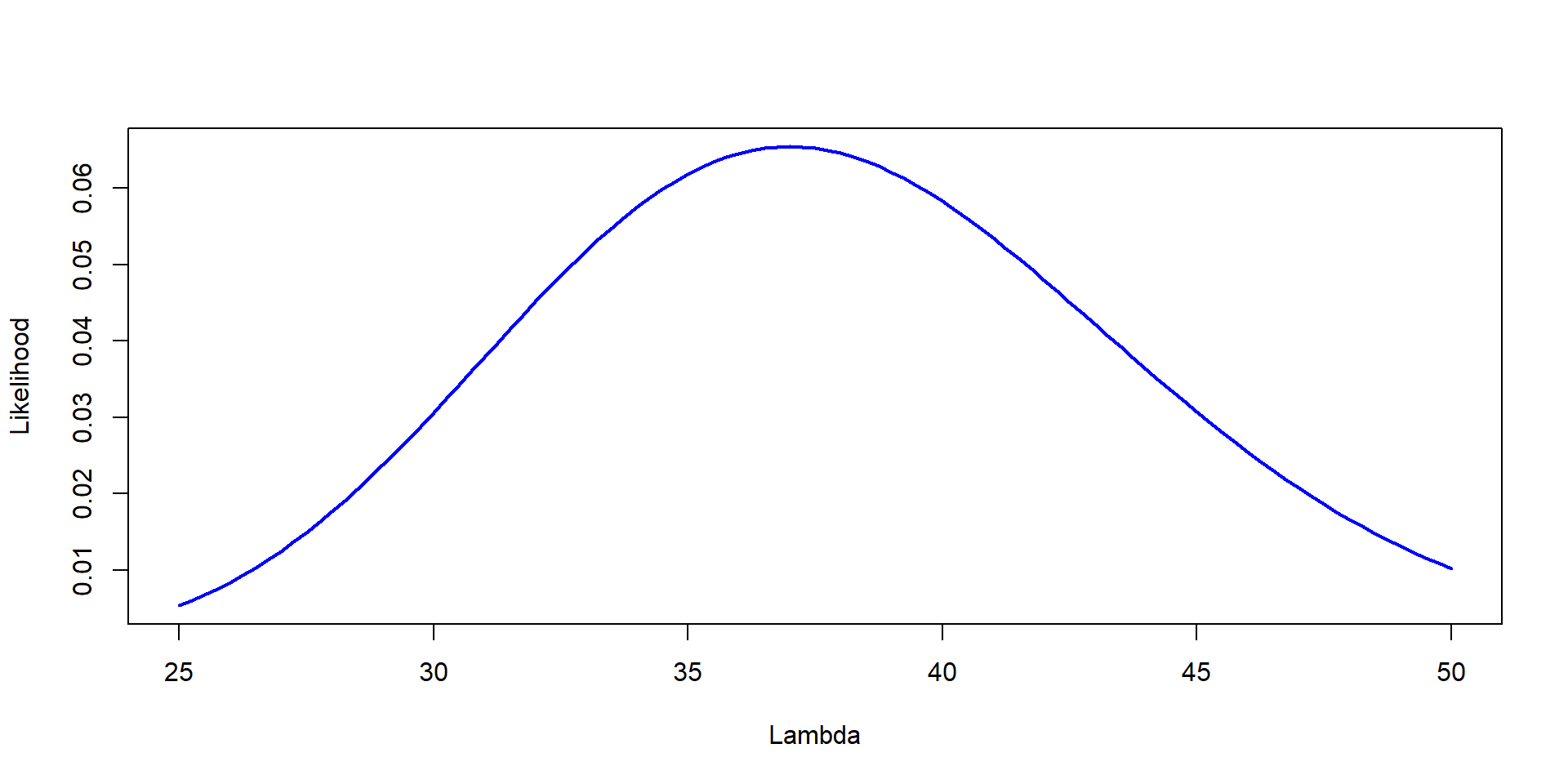
A different statistical framework

We have used frequentist so far

Topic Frequentist Bayesian
Parameters Fixed unknown Random variable
Data Random Fixed
Inference Based on a sampling distribution Based on posterior
Output P-value, Confidence intervals, betas Credible intervals and posterior distribution
Computational needs low high

  • Data, random? Yes…

  • \(y_i = \beta_0 + \beta_1 + \epsilon_i\)

Bayesian take away

Different way of looking at things… we will explore how

Bayes Theorem

\[ \Huge P(\theta |data) = \frac{P(data|\theta) \times P(\theta)}{P(data)} \]

  • \(P(\theta|data)\) : Posterior, probability of theta, given the data
  • \(P(data|\theta)\) : Likelihood! \(\mathcal{L}(\theta|data) = P(data|\theta)\)
  • \(P(\theta)\): Prior (who knows what this is!)
  • \(P(data)\): Marginal (who knows!)

Challenges

  • You go out to a Forest that has been separated in multiple plots. You are wondering what the count of total trees per plot is (\(\lambda\)). You only can count the number of trees in one plot chosen at random. You count 37 trees, Estimate the Likelihood of different values of \(\lambda\) as well as the maximum likelihood.
Lambda=seq(25,50, by=0.25)
Likelihood=dpois(37,Lambda)
plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Lambda")

Answers Q2

  • Challenge 2:

  • You go to the same Forest, but were able to count three plots. They had 37, 41 and 35 trees. Estimate the Likelihood of different values of \(\lambda\)

Lambda=seq(25,50, by=0.25)
Likelihood=dpois(37,Lambda)*dpois(41,Lambda)*dpois(35,Lambda)
plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Lambda")

We usually have more than one n

The more data, the better!

Likelihood=dpois(37,Lambda)
plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Lambda")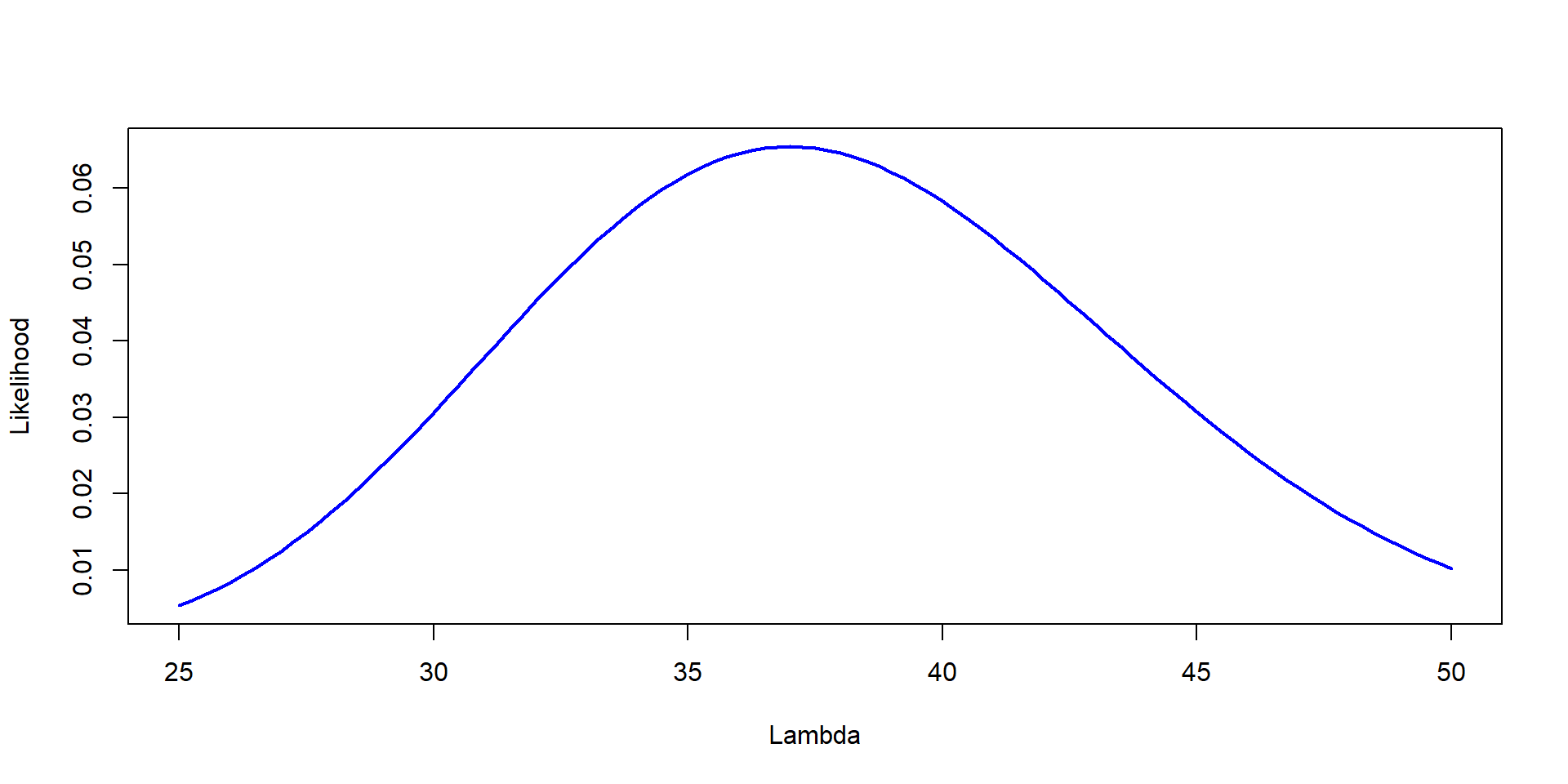

Likelihood=dpois(37,Lambda)*dpois(41,Lambda)*dpois(35,Lambda)
plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Lambda")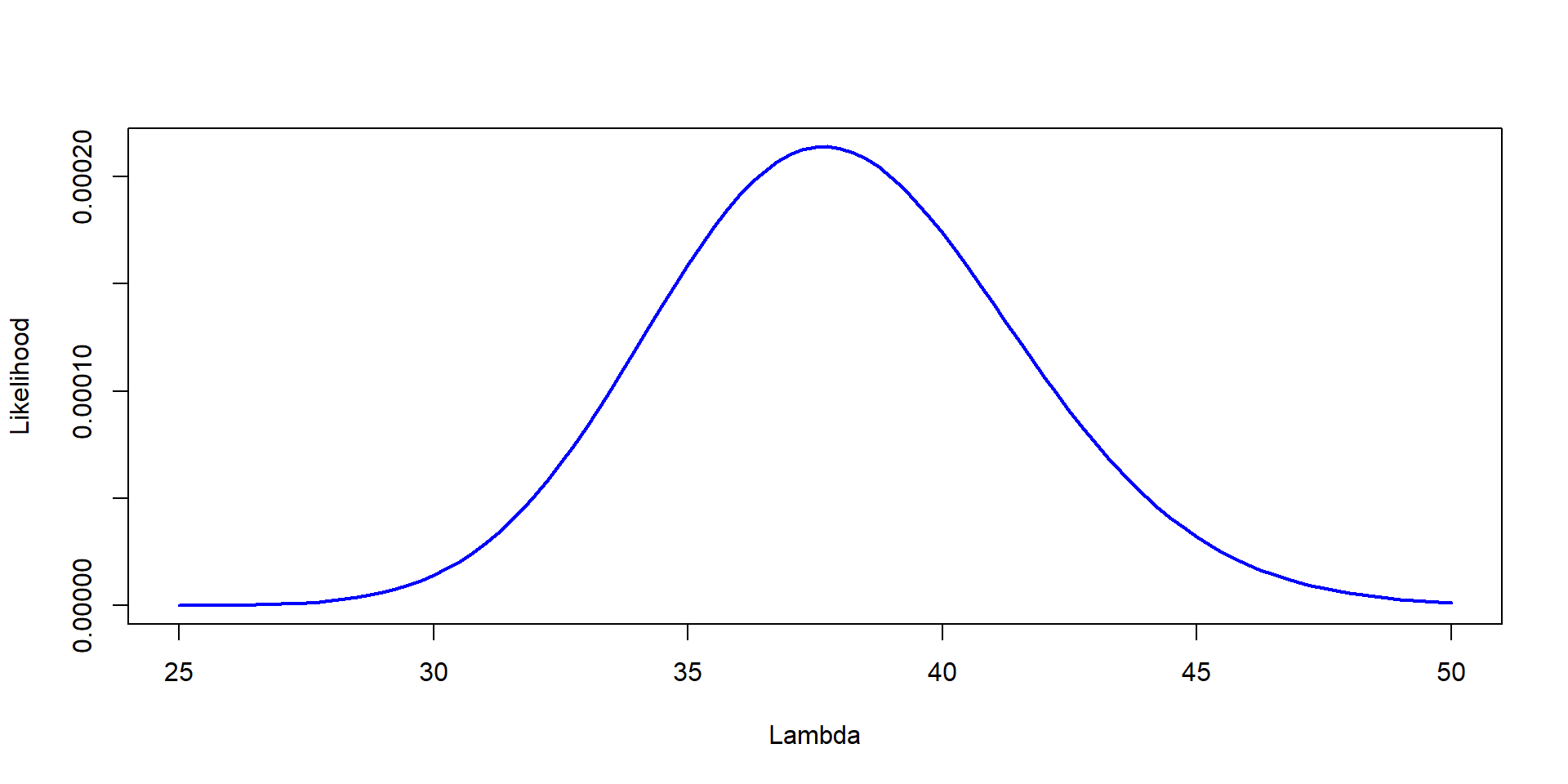

In this case:

\[ \mathcal{L} = P(X_1 = 37 | \lambda) \times P(X_1 = 41 | \lambda) \times P(X_1 = 35 | \lambda) \]

In general:

\[ \mathcal{L}(x_1, x_2, ...,x_n) = \prod_{i=1}^n P(X_i = x_i | \lambda) \]

Hard to compare

Likelihood=dpois(37,Lambda)
plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Lambda")
Likelihood=dpois(37,Lambda)*dpois(41,Lambda)*dpois(35,Lambda)
lines(Lambda,Likelihood, type="l", col="salmon")

Hard to compare

Likelihood=dpois(37,Lambda)
plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Lambda")
Likelihood=dpois(37,Lambda)*dpois(41,Lambda)*dpois(35,Lambda)
lines(Lambda,Likelihood*300, type="l", col="salmon")

Multiple data

forest object with counts of 50 plots

Lambda=seq(25,50, by=0.25)
Likelihood=sapply(Lambda, function(l) prod(dpois(forest, l)))

plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="joint Likelihood", xlab="Lambda")

Dealing with tiny numbers

Lambda=seq(25,50, by=0.25)
Likelihood=sapply(Lambda, function(l) prod(dpois(forest, l)))
scaled_Likelihood<-Likelihood/sum(Likelihood)

plot(Lambda,scaled_Likelihood,type="l", col="blue", lwd=2,ylab="joint Likelihood", xlab="Lambda")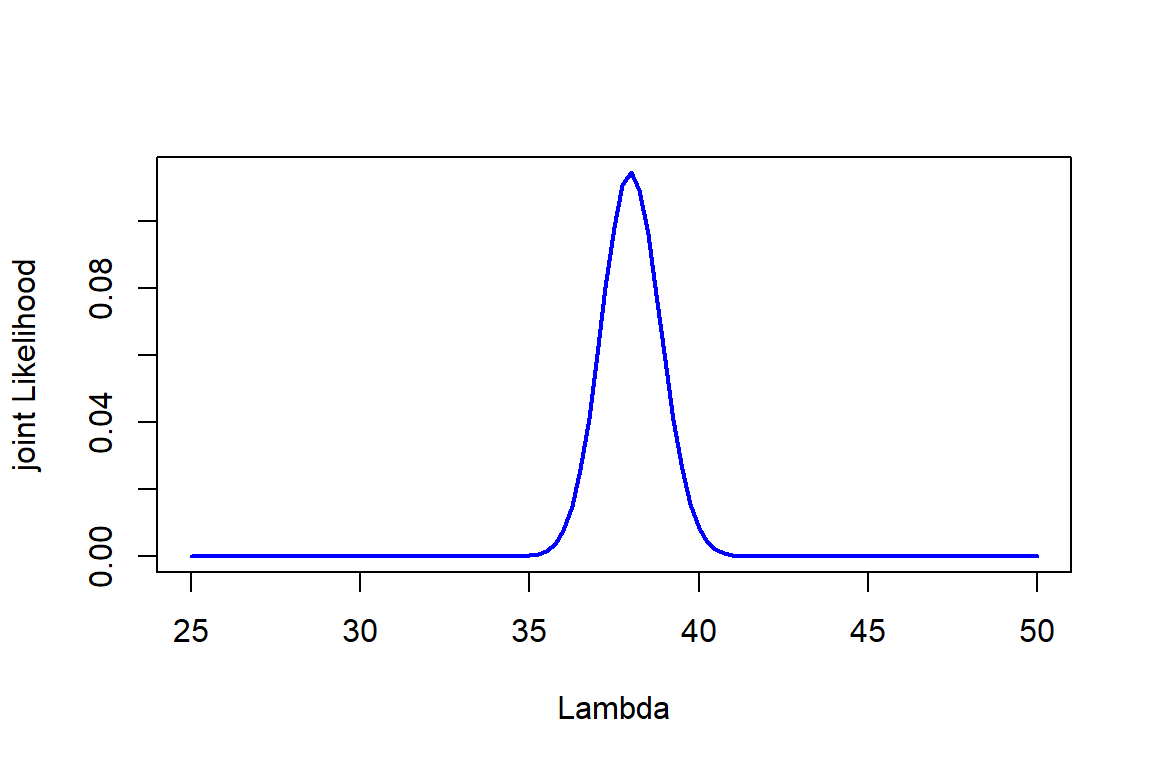

  • Only for plotting!

Bayes Theorem

\[ \Huge P(\theta |data) = \frac{P(data|\theta) \times P(\theta)}{P(data)} \]

  • \(P(\theta|data)\) : Posterior, probability of theta, given the data
  • \(P(data|\theta)\) : Likelihood! \(\mathcal{L}(\theta|data) = P(data|\theta)\)
  • \(P(\theta)\): Prior (who knows what this is!)
  • \(P(data)\): Marginal (who knows!)

Prior

Before talking about priors, I want to tell you all a story

  • I saw a rabbit

  • I saw a fox

  • I saw a cougar

  • I saw a platypus

Data was the same for all 3

So… Likelihood would be the same.

\[ \mathcal{L}(statement = true\ \ | \ \ \text{my thrustworthy professor told me}) \]

  • In each of the four cases, I told you I saw it (think of this as data)

  • So, why did you believe me some times and not other times?

  • Priors!

Priors

The prior distribution provides un with a way of incorporating information about \(\theta\) (population parameter) in our analysis

  • In our lives, any new information is weighed with any prior… so you are all Bayesian

Cleveland Browns and Bayesian Thinking

You check the score: the Browns are up 21 to 7 at halftime against the Ravens. In frequentist probability, you would think:

  • “Probability of winning when going 21-7 is about 80%”

  • \[ \text{Posterior belief} \propto \text{Prior (they find ways to lose)} \times \text{New data (they’re winning now)} \]

  • Essentially, you know that they tend to find ways to lose

  • You may be expecting heartbreak, despite the data (21-7)

Weather

Your weather app says that there is 5% of rain

You get out, and t is overcast, cloudy, and windy… you may get your umbrella

  • This is based on priors! You know that when the sky looks like that, it usually rains

Where do priors come from?

  • Previous studies / historical data

  • Mechanistic limits

  • Theoretical expectations derived from other models

  • Expert knowledge

  • Previous observations

How to incorporate priors?

\[ \Huge P(\theta |data) = \frac{P(data|\theta) \times P(\theta)}{P(data)} \]

Example

  • You go to the same Forest, but were able to count three plots. They had 37, 41 and 35 trees. Estimate the Likelihood of different values of \(\lambda\)
Lambda=seq(25,50, by=0.25)
Likelihood=dpois(37,Lambda)*dpois(41,Lambda)*dpois(35,Lambda)
plot(Lambda,Likelihood,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Lambda")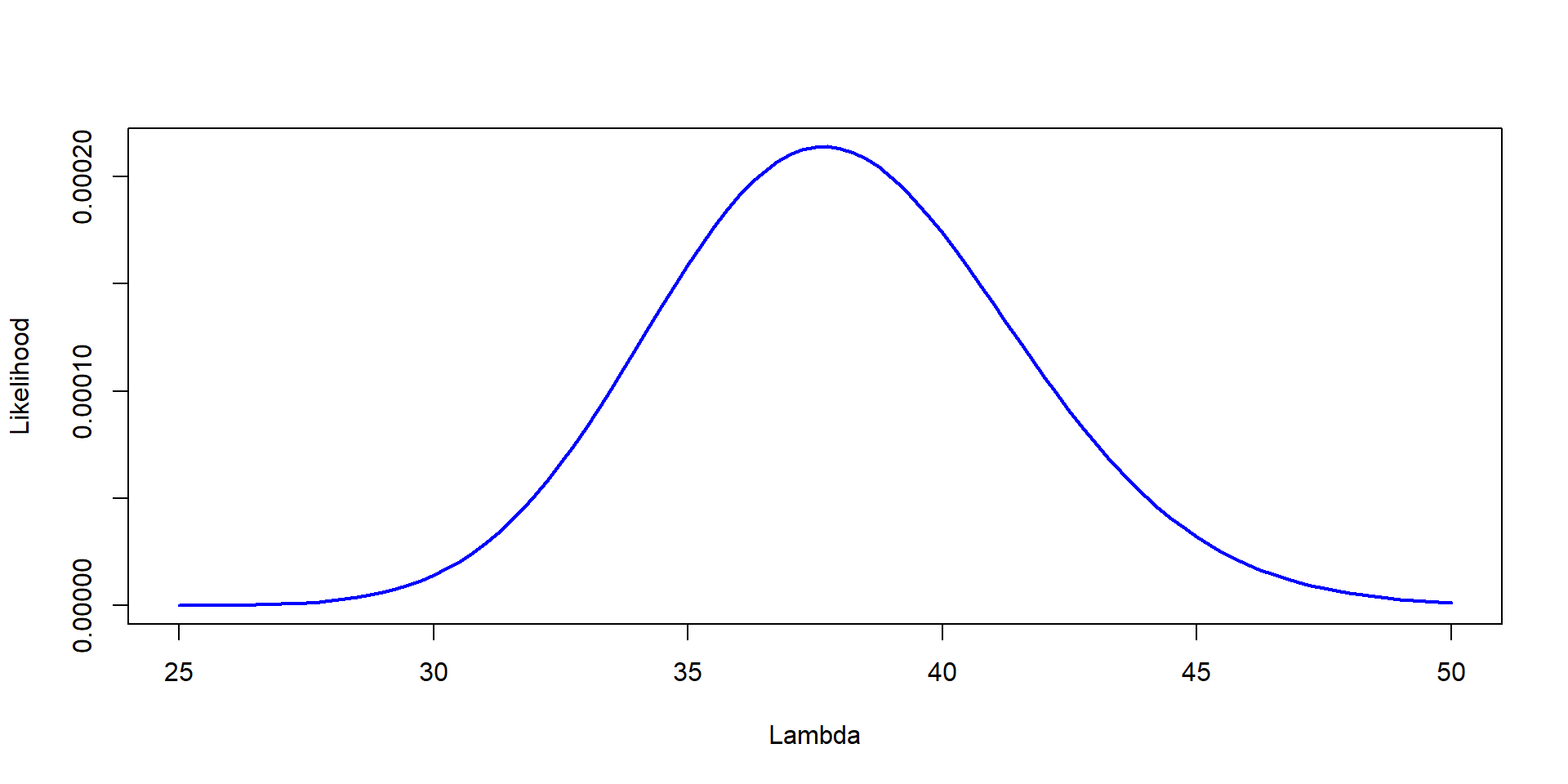

  • This is the Likelihood

  • \[ P(\theta | data) = \frac{P(data|\theta) \times P(\theta)}{P(data)} \]

  • Joint Likelihood: We need to multiply it by the priors

  • A prior study (one year ago), you counted trees per plots. And found a mean of 39.9 and a sd of 6.75

Using the prior information

  • There are specific methods (momentum matching) to transform priors.

  • For normal:

    • \(\theta \sim N(\mu, \sigma^2)\)

  • For counts:

    • \(\lambda \sim \gamma(\alpha, \beta)\)

    • \(\beta = \frac{\mu}{\sigma^2}\)

    • \(\alpha = \mu \times \beta\)

    • That’s it!

In this example

Likelihood:

Lambda=seq(25,50, by=0.25)
Likelihood=dpois(37,Lambda)*dpois(41,Lambda)*dpois(35,Lambda)
Likelihood_scaled=Likelihood/sum(Likelihood)

A prior study (one year ago), you counted trees per plots. And found a mean of 43.2 and a sd of 4.05

# Example prior as Gamma
mu <- 43.2
sigma <- 4.05

beta <- mu / sigma^2
alpha <- mu * beta

prior <- dgamma(Lambda, shape = alpha, rate = beta)

Together

plot(Lambda,Likelihood_scaled,type="l", col="blue", lwd=2,ylab="joint Likelihood", xlab="Lambda")
lines(Lambda, prior, col="salmon", lty=2,lwd=2)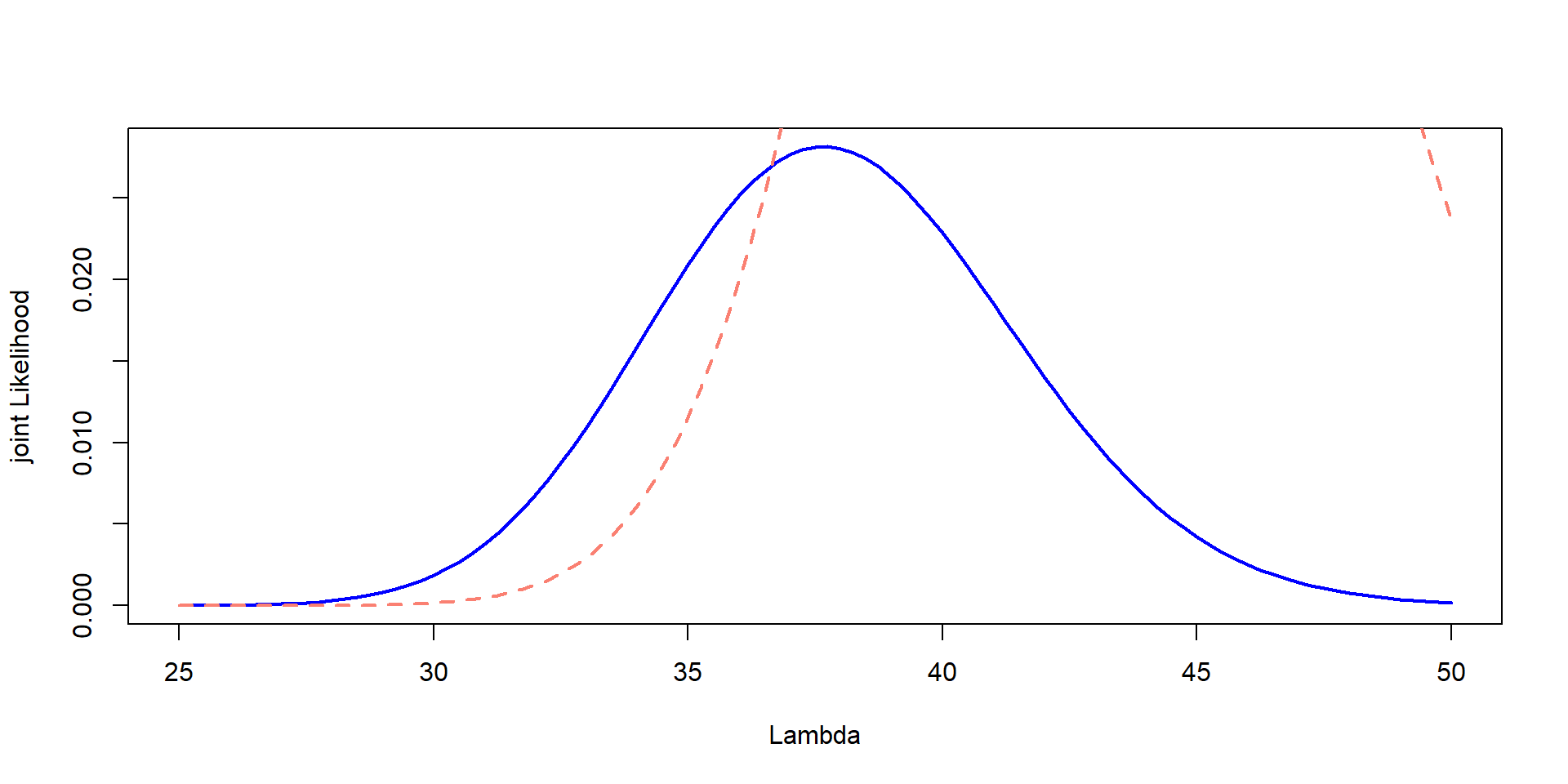

  • Issue! They are in different scales

  • But… we can change the scaling,just for plotting!!

prior_scaled <- prior * max(Likelihood_scaled) / max(prior)
plot(Lambda,Likelihood_scaled,type="l", col="blue", lwd=2,ylab="joint Likelihood", xlab="Lambda")
lines(Lambda, prior_scaled, col="salmon", lty=2)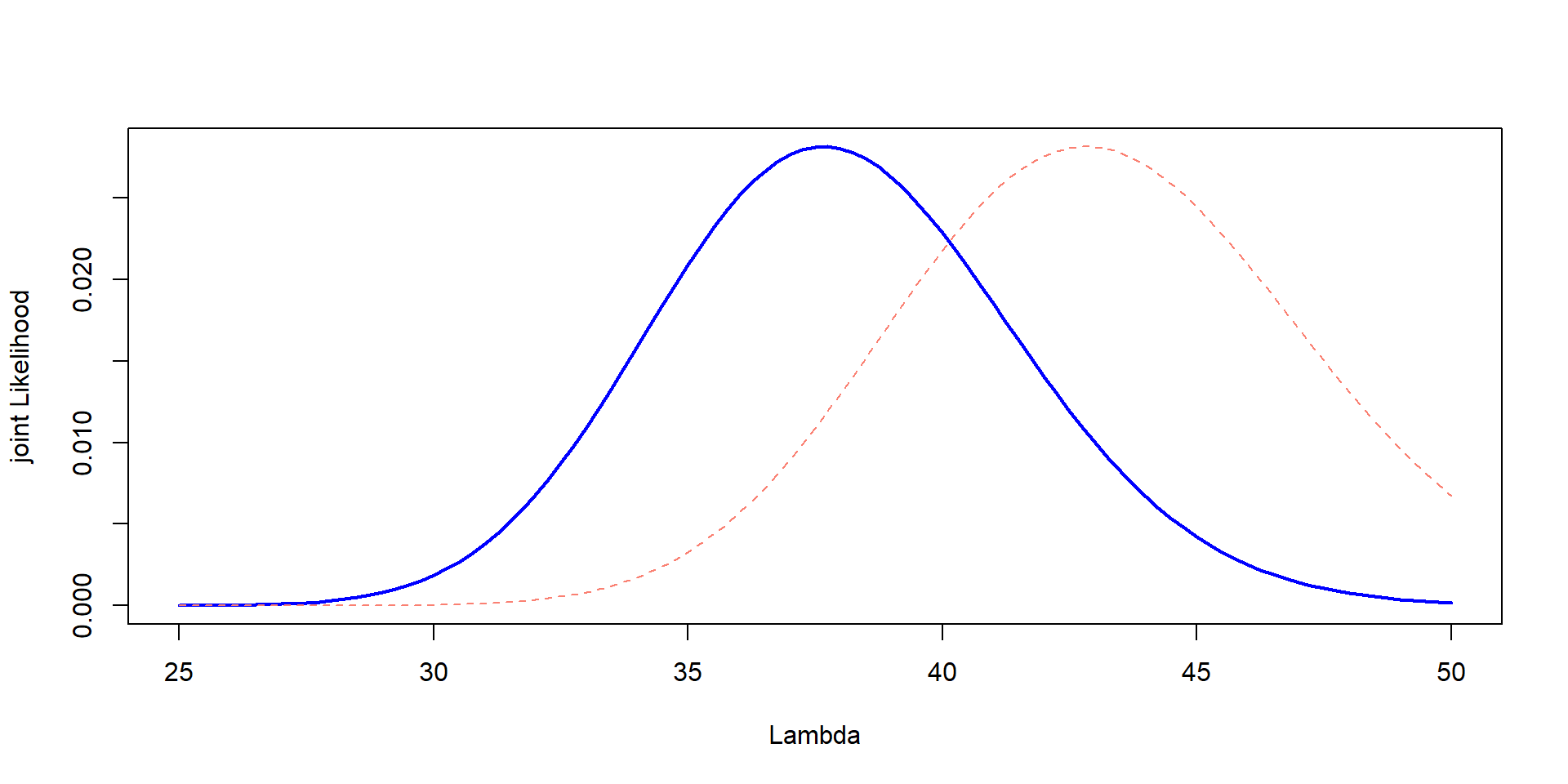

  • JUST FOR PLOTS!!!

Joint Likelihood

\[ P(data|\theta) \times P(\theta) \]

Multiply them! The original numbers!

  • Scaling is good… but just for plotting, we need to use the actual estimates!

Multiply them

jointL<- prior * Likelihood

That’s it! We have our joint Likelihood!

We cannot plot it

It is in different scales!

plot(Lambda,Likelihood_scaled,type="l", col="blue", lwd=2,ylab="joint Likelihood", xlab="Lambda")
lines(Lambda, prior_scaled, col="salmon", lty=2)
lines(Lambda,jointL)

Scale it (for plots)

jointL_scaled <- jointL * max(Likelihood_scaled) / max(jointL)

prior_scaled <- prior * max(Likelihood_scaled) / max(prior)
plot(Lambda,Likelihood_scaled,type="l", col="blue", lwd=2,ylab="joint Likelihood", xlab="Lambda")
lines(Lambda, prior_scaled, col="salmon", lty=2)
lines(Lambda,jointL_scaled, lwd=3, lty=3)

Final step

\[ P(\theta | data) = \frac{P(data|\theta) \times P(\theta)}{P(data)} \] \(P(data)\) is the marginal likelihood

The point of the maginal likelihood is “standardizing” the joint likelihood

This way, the area under the curve sums to 1.

Posterior<- jointL/sum(jointL)
  • That’s it!

Plot it

plot(Lambda,Posterior,type="l", col="blue", lwd=2,ylab="joint Likelihood", xlab="Lambda")

That is the result

  • No point estimate. It models “uncertainty”

  • Median is usually reported

  • You can estimate 95% of the area under the curve –> credible intervals

Challenge. Bats per net

  • You are surveying bats near a beach. You set up one mist net and caught 8 bats

  • From previous surveys, you know that the mean catch per net is around 10 bats, with a standard deviation of around 3 bats

  • Estimate Likelihood, prior, combine them (joint) and estimate the posterior (normalized so that it sums to 1)

  • Plot all three on the same graph: likelihood, prior, and posterior –> Scale the prior and likelihood if necessary so they fit on the same plot

  • Find the most probable value of \(\lambda\)

For next class

Download JAGS