Bayesian statistics

SNR 610

Today

Probability and Likelihood (step 1 out of 3)

Reminder

  • What is probability?

  • Certainty that an event will happen

  • Example:

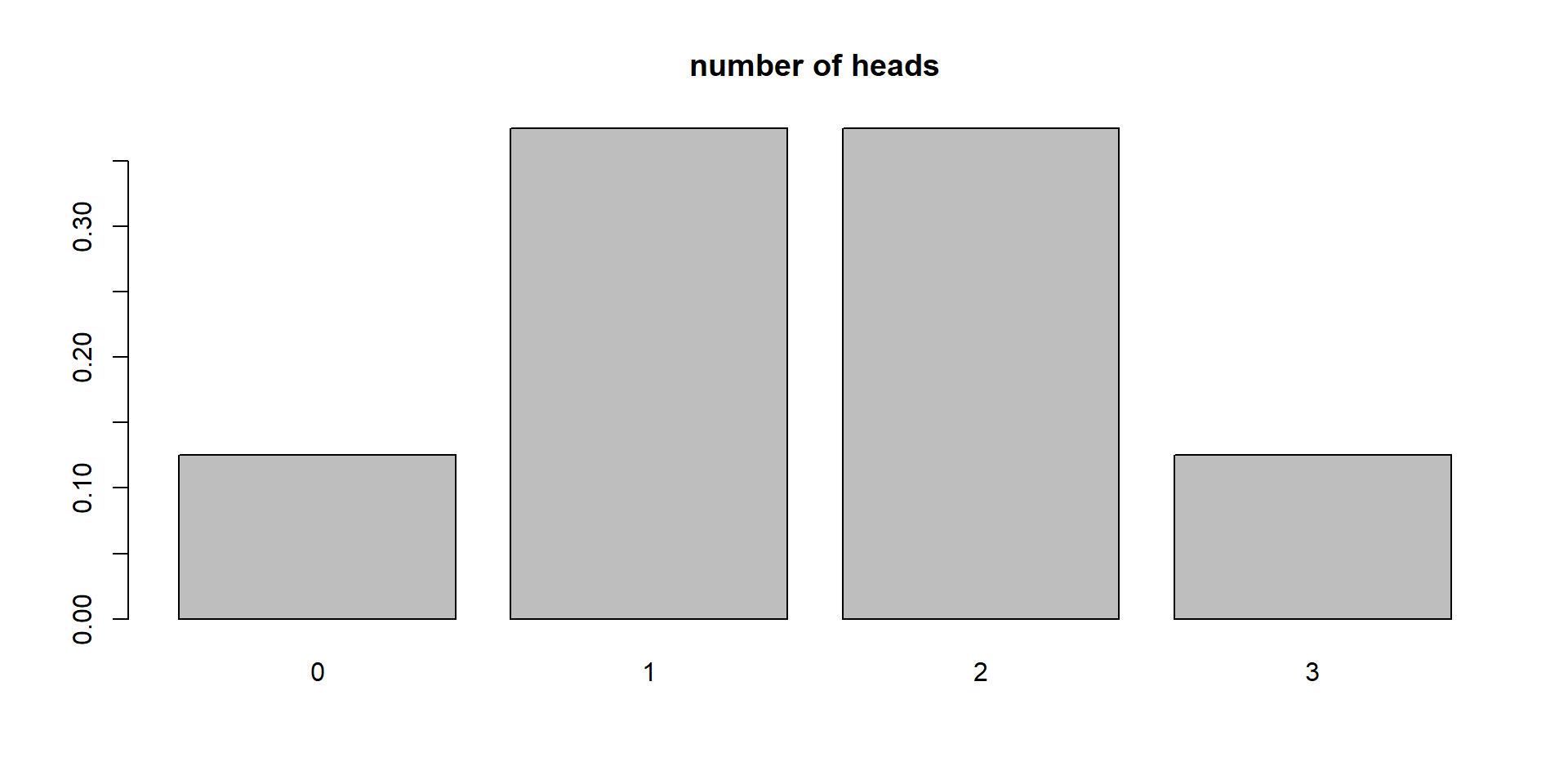
    • X = number of heads in 3 tosses

    • x = exactly 2 heads

    • \(\theta=0.5\) (probability)

    • \(P(X=x | \theta) = 3/8\)

    • \(P(\text{Number of heads in 3 tosses}= 2 | 0.5) = 3/8\)

Why?

flowchart LR
  A[HEADS] --> B[HEADS]
  A --> C[TAILS]
  B --> D[HEADS]
  B --> E[TAILS]
  C --> F[HEADS]
  C --> G[TAILS]


flowchart LR
  A[TAILS] --> B[HEADS]
  A --> C[TAILS]
  B --> D[HEADS]
  B --> E[TAILS]
  C --> F[HEADS]
  C --> G[TAILS]

Probability

  • 3 tosses

  • Probability of 1 head?

  • Probability of 3 heads?

  • Probability of 0 heads?

  • We treat \(\theta\) as fixed (0.5)

Probability

We can actually estimate any probability as long as we know the parameters

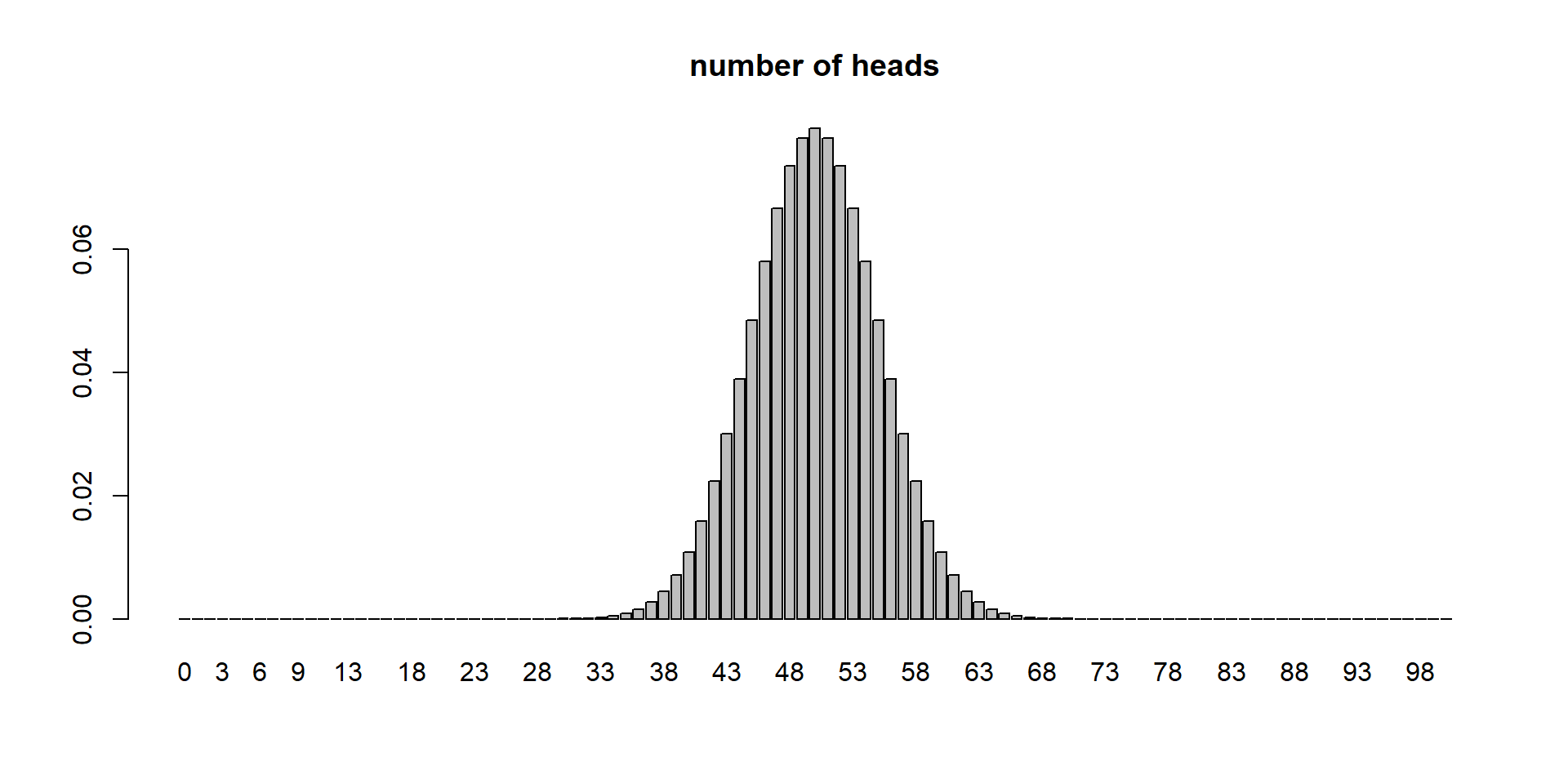
  • Binomial distribution parameters: n and p

  • n is number of trials

  • \(P(X=x | \theta) = Y\)

  • \(P(successes = x | \text{p and n}) = Y\)

  • \(P(successes = 12 | \text{0.5 and 50}) = 0.0001078\)

  • \(P(successes \ge 57 | \text{0.5 and 100}) = 0.0966\)

  • We use dbinom. Like this: dbinom(x,n,p) Example: dbinom(12,50,0.5)

  • For \(\ge\) 57: sum(dbinom(57:n,n,p))

Probability

dbinom(2,3,0.5)
[1] 0.375
dbinom(1,3,0.5)
[1] 0.375

Probability

dbinom(0:3,3,0.5)
[1] 0.125 0.375 0.375 0.125

Probability

dbinom(0:100,100,0.5)

Parameters of binomial

Probability and n!

Parameters of a Normal distribution

Who can remember them?

  • Mean and sd (or variance)

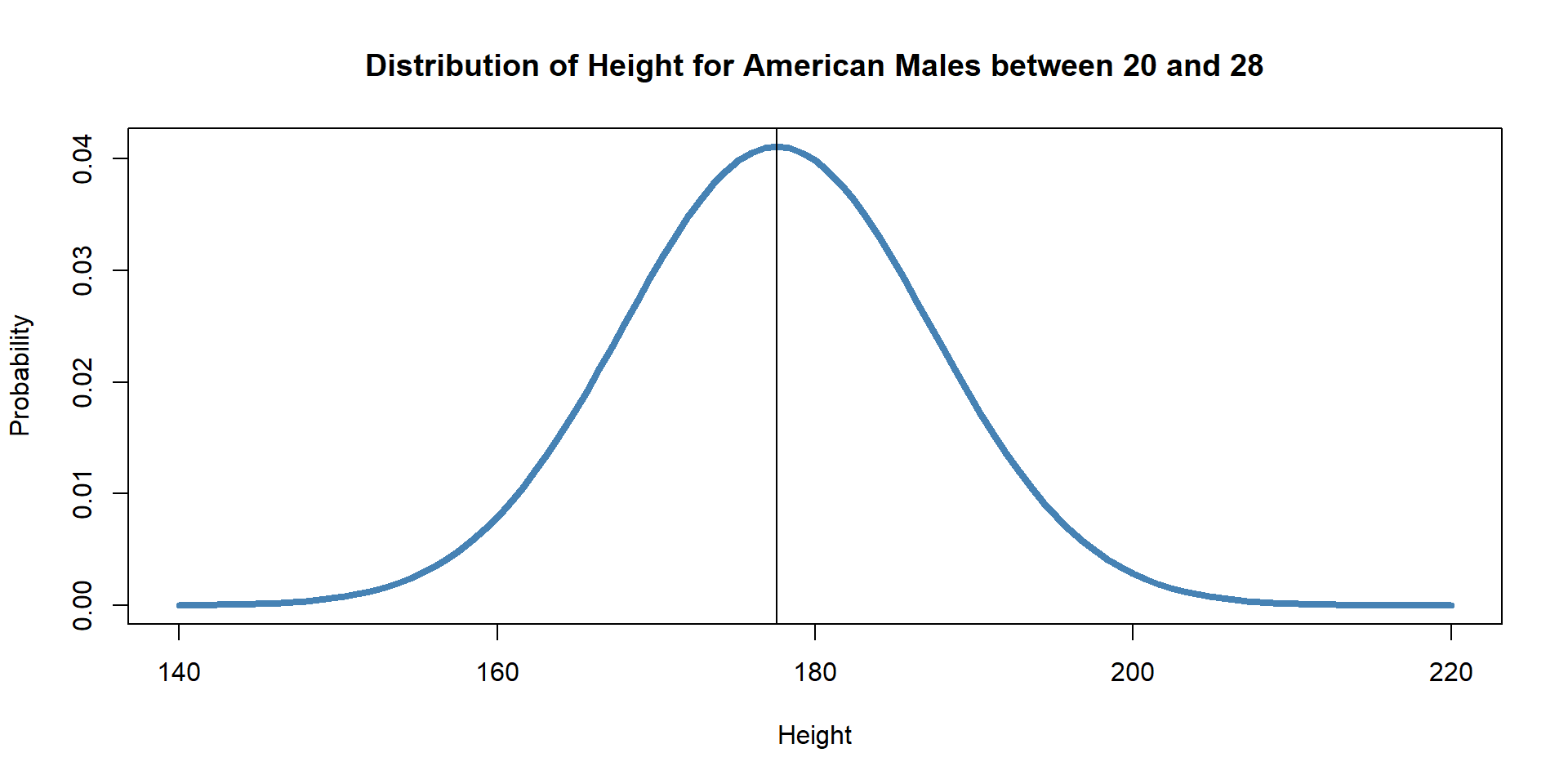
  • For a population of males in the USA, these are the parameters:

    • \(\mu = 177.6cm\)

    • \(\sigma = 9.7cm\)

  • What is the probability of sampling a random man with a heigh of 172.85431 cm?

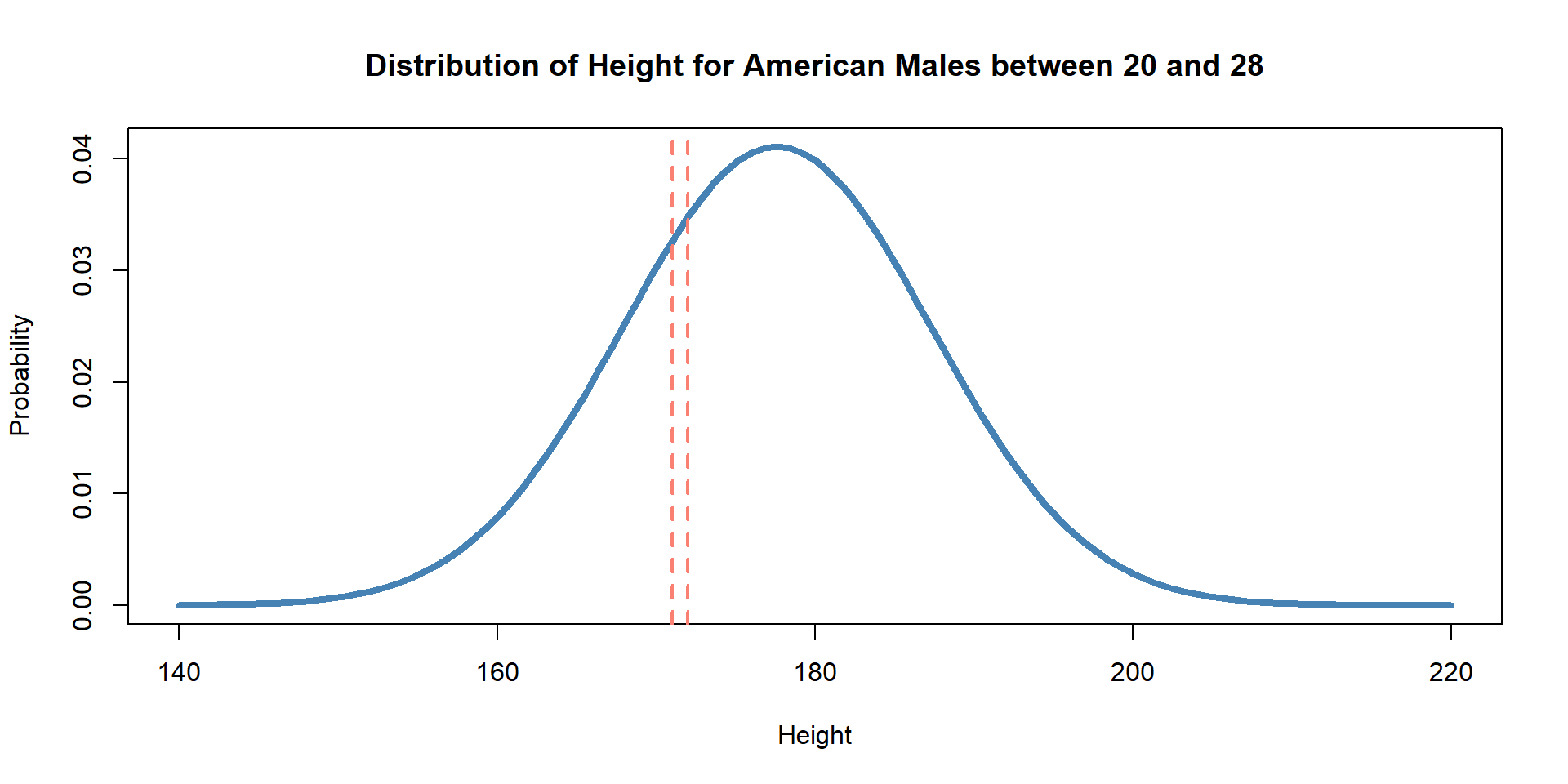
  • What is the probability of sampling one random man and him being between 170 and 171 cm?

pnorm(171,177.7,9.7)-pnorm(170,177.7,9.7)
[1] 0.03121851

Normal Distribution

By knowing the mean and sd we can plot any normal distibution

We can estimate any probability as well

Probability of observing X given the parameters

  • \(P ( 170 \le X \le 171) | \mu = 177.6, \sigma = 9.7)\)

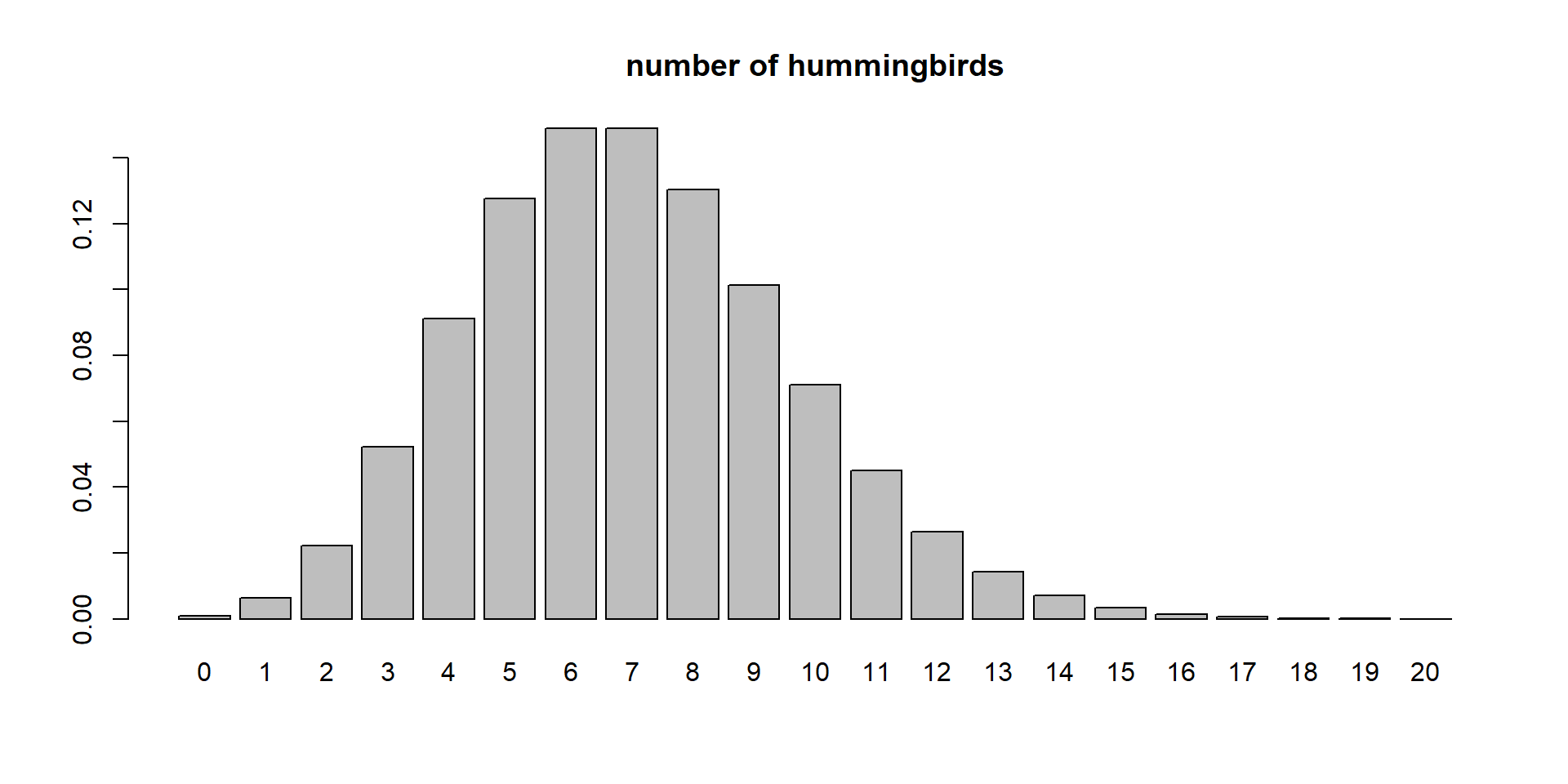
Poisson Distribution

  • One parameter

  • \(\lambda\)

  • Represents both mean and sd

  • When \(\lambda = 7\) what is the probability of seeing 5 hummingbirds visit a flower?

  • \(P(X=5|\lambda =7)\)

Poisson Distribution

dpois(5,7)
[1] 0.1277167
barplot(dpois(0:20,7), names.arg = 0:20, main="number of hummingbirds")

Takeaway

Probability: Chance of an event occuring

  • Chance of data being something, given the parameters

  • The parameters do not change. For example, for a p of 0.5 we can estimate the prob of 0, 1, 2… 100 heads out of 100

Question

Test your knowledge…

  • You have a coin that you do not know if it is fair or unfair. What is the probability that you will get 40 heads in 100 tosses?

Probability

We cannot estimate it if we do not have the parameters!

  • We usually do not have them

  • It is what we are trying to estimate!!!!

  • If we had them, there would be no point on sampling/experiments

  • Examples:

    • Probability of infection (infection rate)

    • Yield of a crop

    • Annual sales

    • community composition

What do we have?

Data!

Unfair or fair coin

You are smart, so you knew we couldn’t estimate it! You decide to grab the coin, and do 100 flips.

  • You get 65 heads and 35 tails

  • What value of P (prob of heads) is more likely:

    • 0.3

    • 0.5

    • 0.7

We can estimate the Likelihood

Likelihood of a parameter given our data

  • Probability: \(P(X=x|\theta)\)

  • x = data and \(\theta\) = parameter

  • Likelihood: \(\mathcal{L}(x|\theta = y)\)

In other words

  • Likelihood: \(\mathcal{L}(65|p= 0.3 \; \& \; n=100)\)

  • Likelihood: \(\mathcal{L}(65|p= 0.5 \; \& \; n=100)\)

  • Likelihood: \(\mathcal{L}(65|p= 0.7 \; \& \; n=100)\)

In other words

Likelihood: \(\mathcal{L}(65|p= 0.3 \; \& \; n=100)\)

Likelihood: \(\mathcal{L}(65|p= 0.5 \; \& \; n=100)\)

Likelihood: \(\mathcal{L}(65|p= 0.7 \; \& \; n=100)\)

dbinom(65,100,0.3)  
[1] 4.273205e-13

In other words

Likelihood: \(\mathcal{L}(65|p= 0.3 \; \& \; n=100)\)

Likelihood: \(\mathcal{L}(65|p= 0.5 \; \& \; n=100)\)

Likelihood: \(\mathcal{L}(65|p= 0.7 \; \& \; n=100)\)

dbinom(65,100,0.3)  
[1] 4.273205e-13
dbinom(65,100,0.5)     
[1] 0.0008638557
dbinom(65,100,0.7)
[1] 0.04677968

In other words

Likelihood: \(\mathcal{L}(65|p= 0.3 \; \& \; n=100)\)

Likelihood: \(\mathcal{L}(65|p= 0.5 \; \& \; n=100)\)

Likelihood: \(\mathcal{L}(65|p= 0.7 \; \& \; n=100)\)

dbinom(65,100,0.3)  
[1] 4.273205e-13
dbinom(65,100,0.5)     
[1] 0.0008638557
dbinom(65,100,0.7)
[1] 0.04677968
dbinom(65,100,seq(0.01,0.99, by=0.01))
 [1] 7.703225e-104  1.992063e-84  3.884481e-73  3.571358e-65  4.929663e-59
 [6]  4.772511e-54  7.374228e-50  2.970735e-46  4.282059e-43  2.741123e-40
[11]  9.091081e-38  1.750311e-35  2.132713e-33  1.758769e-31  1.035226e-29
[16]  4.539569e-28  1.535868e-26  4.127038e-25  9.024029e-24  1.638853e-22
[21]  2.515609e-21  3.313036e-20  3.792499e-19  3.816341e-18  3.409459e-17
[26]  2.727838e-16  1.969634e-15  1.292261e-14  7.750912e-14  4.273205e-13
[31]  2.176051e-12  1.028019e-11  4.523399e-11  1.860408e-10  7.175152e-10
[36]  2.602570e-09  8.901681e-09  2.877953e-08  8.814231e-08  2.562323e-07
[41]  7.082912e-07  1.864766e-06  4.682851e-06  1.123170e-05  2.576014e-05
[46]  5.655635e-05  1.189753e-04  2.400149e-04  4.646673e-04  8.638557e-04
[51]  1.542997e-03  2.649119e-03  4.373180e-03  6.943193e-03  1.060361e-02
[56]  1.557780e-02  2.201417e-02  2.992165e-02  3.910718e-02  4.913282e-02
[61]  5.931182e-02  6.875851e-02  7.649566e-02  8.160685e-02  8.340469e-02
[66]  8.157530e-02  7.625895e-02  6.804079e-02  5.784834e-02  4.677968e-02
[71]  3.590570e-02  2.609661e-02  1.791259e-02  1.157630e-02  7.019775e-03
[76]  3.978485e-03  2.098032e-03  1.024198e-03  4.601262e-04  1.889469e-04
[81]  7.036278e-05  2.354392e-05  7.002111e-06  1.827232e-06  4.119694e-07
[86]  7.876283e-08  1.247985e-08  1.592788e-09  1.579556e-10  1.161994e-11
[91]  5.965119e-13  1.966976e-14  3.709060e-16  3.373223e-18  1.136123e-20
[96]  9.102708e-24  7.565670e-28  1.012012e-33  5.698078e-44

Likelihood

x=seq(0.01,0.99, by=0.01)
y=dbinom(65,100,seq(0.01,0.99, by=0.01))
plot(x,y,type="l", col="blue", lwd=2,ylab="Likelihood", xlab="Probability")
abline(v=0.5)

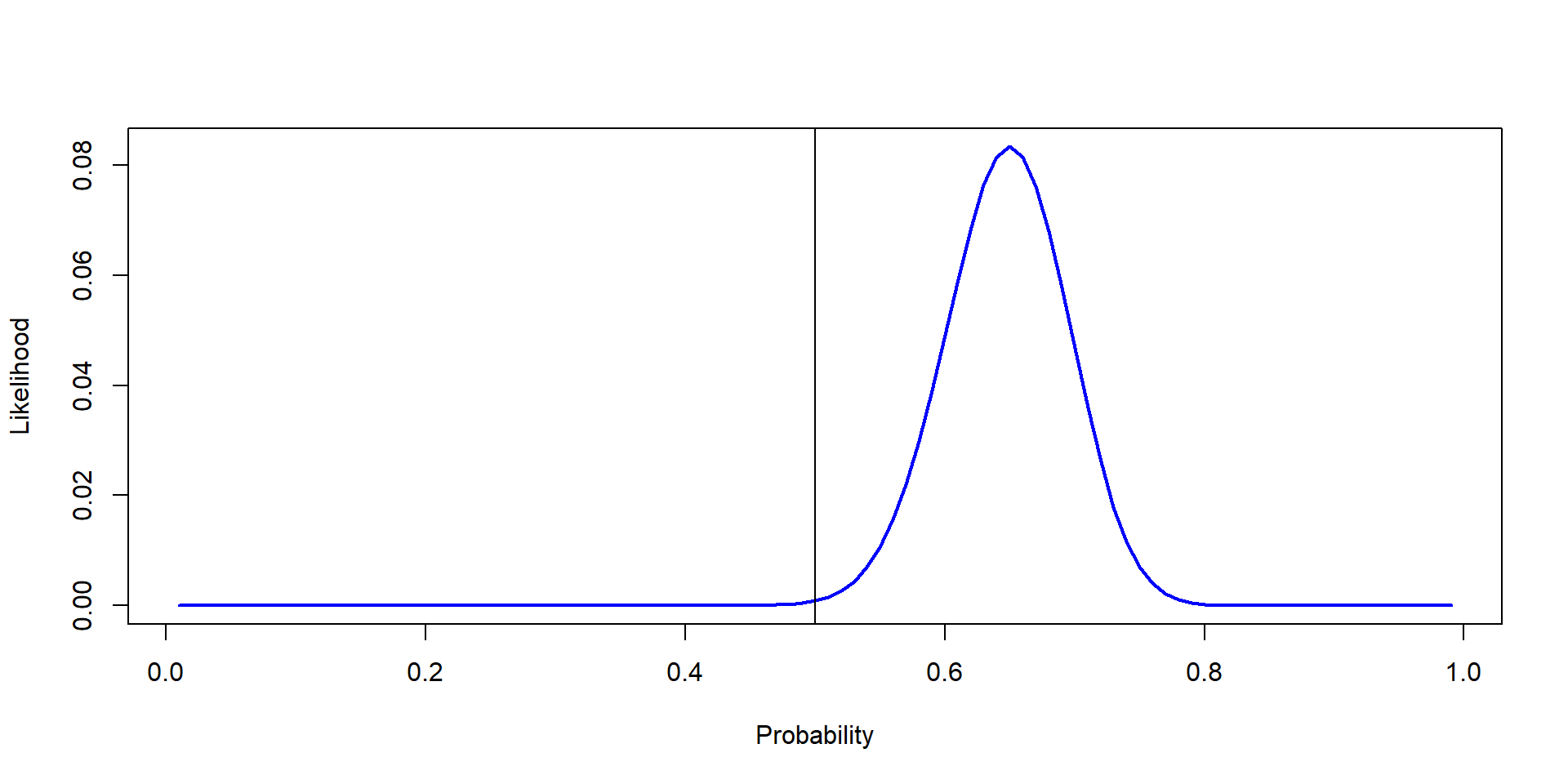
“Very Unlikely that it is fair”

Probability vs Likelihood

Probability:

dbinom(0:100,100,0.5)

Likelihood

dbinom(65,100,seq(0.01,0.99, by=0.01))

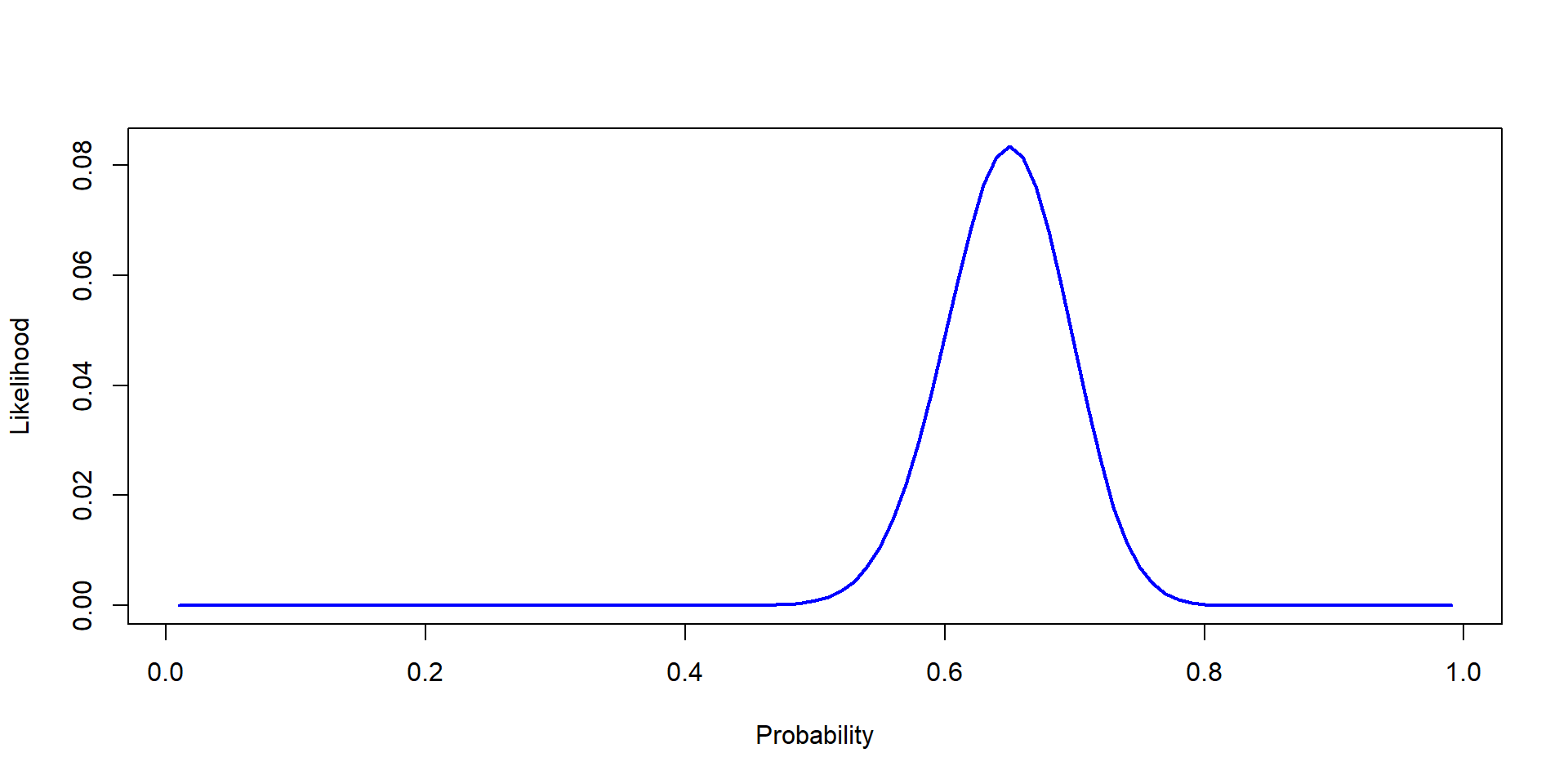
Likelihood is continuous

Review

  • If you capture 5 raccoons with weights of 11.2, 12, 11.5, 12.8, 11.06 is it more likely that the population mean is 11.5 or 17?

  • If you get 80 heads in 100 tosses, is it more likely that p is 0.8 or 0.5

  • If you count insects per tree and find 77, 70, 75, 86, and 90 is it more likely that \(\lambda\) for insects per tree is 60, 80, or 120?

  • Likelihood is estimated!

  • \(\mathcal{L}(x|\theta = y)\)

  • And usually (and correctly): \(\mathcal{L}(\theta|data)\)

  • We use the probability density functions

Likelihood and probability (correct way)

\[ \Huge \mathcal{L}(\theta|data) \]

\[ \Huge P(data|\theta) \]

\[ \mathcal{L}(\theta|data) = P(data|\theta) \]

  • Likelihood of p being 0.5 given 48 heads out of 100 tosses
dbinom(65,100,0.5)  
[1] 0.0008638557
  • Probability of 48 heads out of 100 tosses given a probability of 0.5
dbinom(65,100,0.5)  
[1] 0.0008638557

Bayesian

A different statistical framework

We have used frequentist so far

Topic Frequentist Bayesian
Parameters Fixed unknown Random variable
Data Random Fixed
Inference Based on a sampling distribution Based on posterior
Output P-value, Confidence intervals, betas Credible intervals and posterior distribution
Computational needs low high

  • Data, random? Yes…

  • \(y_i = \beta_0 + \beta_1 + \epsilon_i\)

Bayesian take away

Different way of looking at things… we will explore how

Bayes Theorem

\[ \Huge P(\theta |data) = \frac{P(data|\theta) \times P(\theta)}{P(data)} \]

  • \(P(\theta|data)\) : Posterior, probability of theta, given the data
  • \(P(data|\theta)\) : Likelihood! \(\mathcal{L}(\theta|data) = P(data|\theta)\)
  • \(P(\theta)\): Prior (who knows what this is!)
  • \(P(data)\): Marginal (who knows!)

Challenges

  • Challenge 1:

    • You go out to a Forest that has been separated in multiple plots. You are wondering what the count of total trees per plot is (\(\lambda\)). You only can count the number of trees in one plot chosen at random. You count 37 trees, Estimate the Likelihood of different values of \(\lambda\) as well as the maximum likelihood.

  • Challenge 2:

    • You go to the same Forest, but were able to count three plots. They had 37, 41 and 35 trees. Estimate the Likelihood of different values of \(\lambda\)